
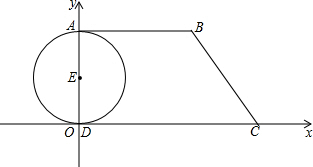
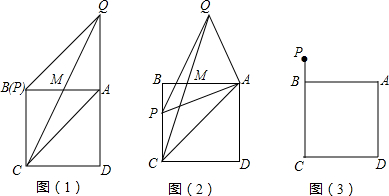
 如图,在平面直角坐标系中,直角梯形ABCD的直角顶点D与原点重合,另一直角顶点A在y轴的正半轴上,点B、C的坐标分别为B(12,8)、C(14,0),AD为⊙E的直径.点M、N分别从A、C两点同时出发做匀速运动,其中点M沿AB向终点B运动,速度为每秒1个单位;点N沿CD向终点D运动,速度为每秒3个单位.当这两点中有一点到达自己的终点时,另一点也停止运动.
如图,在平面直角坐标系中,直角梯形ABCD的直角顶点D与原点重合,另一直角顶点A在y轴的正半轴上,点B、C的坐标分别为B(12,8)、C(14,0),AD为⊙E的直径.点M、N分别从A、C两点同时出发做匀速运动,其中点M沿AB向终点B运动,速度为每秒1个单位;点N沿CD向终点D运动,速度为每秒3个单位.当这两点中有一点到达自己的终点时,另一点也停止运动.分析 (1)根据平行四边形的对边相等即可得出t的值;
(2)连接AP,求出AM的长,利用勾股定理求出OM的长,再根据△OAM∽△OPA即可得出结论;
(3)假设存在MN与⊙E相切,切点为F,可知MF=MA=t,FN=DN=14-3t,连接EF,EM,EN,根据△EMF∽△NEF即可求出t的值,进而得出M、N的坐标,利用待定系数法求出直线MN的解析式即可.
解答 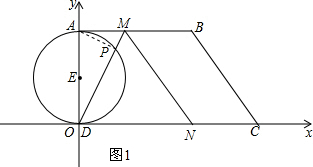 解:(1)∵四边形MBCN为平行四边形,
解:(1)∵四边形MBCN为平行四边形,
∴BM=CN,即12-t=3t,解得t=3;
(2)如图1,连接AP,
∵AM=3,OA=8,
∴OM=$\sqrt{{AM}^{2}+{OA}^{2}}$=$\sqrt{{3}^{2}+{8}^{2}}$=$\sqrt{73}$.
∵OA是⊙O的直径,
∴∠APO=90°.
∵∠APO=∠OAM,∠AOM=∠AOM,
∴△OAM∽△OPA,
∴$\frac{OA}{OM}$=$\frac{OP}{OA}$,即$\frac{8}{\sqrt{73}}$=$\frac{OP}{8}$,解得OP=$\frac{{64\sqrt{73}}}{73}$;
(3)存在.
如图2,假设存在MN与⊙E相切,切点为F,可知MF=MA=t,FN=DN=14-3t,连接EF,EM,EN,
∵MF=MA,FN=DN,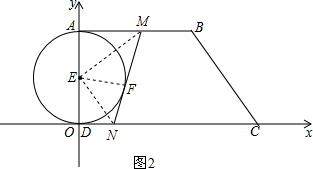
∴∠MEF=$\frac{1}{2}$∠AEF,∠NEF=$\frac{1}{2}$∠OEF,
∴∠MEN=90°.
∵EF⊥MN,
∴∠MFE=∠NFE=90°,∠MEF+∠EMF=90°,
∴∠MEF=∠NEF,
∴△EMF∽△NEF,
∴$\frac{NF}{EF}$=$\frac{EF}{MF}$,即$\frac{14-3t}{4}$=$\frac{4}{t}$,即42=t(14-3t),解得:t1=2,t1=$\frac{8}{3}$.
∴M1(2,8),N1(8,0)和M2($\frac{8}{3}$,8),N2(6,0)
设直线MN的解析式为y=kx+b,将M1(2,8),N1(8,0)代入 得M1N1:y=-$\frac{4}{3}$x+$\frac{32}{3}$;
将M2($\frac{8}{3}$,8),N2(6,0)代入得M2N2:y=-$\frac{12}{5}$x+$\frac{72}{5}$.
综上所述,直线MN的解析式为:y=-$\frac{4}{3}$x+$\frac{32}{3}$或y=-$\frac{12}{5}$x+$\frac{72}{5}$.
点评 本题考查的是圆的综合题,涉及到相似三角形的判定与性质、平行四边形的判定及待定系数法求一次函数的解析式等知识,根据题意作出辅助线,构造出相似三角形是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com