
分析 (1)设A型空调购进x台,B型空调购进40-x台,根据题意列出解析式解答即可;
(2)把y=17000元代入解析式解答即可;
(3)根据题意列出不等式解答即可.
解答 解:(1)设A型空调购进x台,B型空调购进40-x台,可得:
y=(3000-2500)x+(3200-2800)(40-x)=100x+16000;
(2)把y=17000代入解析式y=100x+16000,
解得:x=10,40-x=30,
答:购进A型和B型空调各10台、30台;
(3)根据题意可得:100x+16000≤18400,
解得:x≤2.4.
答:至多要购进38台B型空调.
点评 此题考查一次函数的应用,关键是设A型空调购进x台,B型空调购进40-x台,再根据题意列出解析式进行分析.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 等边三角形 | C. | 锐角三角形 | D. | 直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
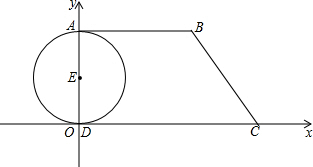 如图,在平面直角坐标系中,直角梯形ABCD的直角顶点D与原点重合,另一直角顶点A在y轴的正半轴上,点B、C的坐标分别为B(12,8)、C(14,0),AD为⊙E的直径.点M、N分别从A、C两点同时出发做匀速运动,其中点M沿AB向终点B运动,速度为每秒1个单位;点N沿CD向终点D运动,速度为每秒3个单位.当这两点中有一点到达自己的终点时,另一点也停止运动.
如图,在平面直角坐标系中,直角梯形ABCD的直角顶点D与原点重合,另一直角顶点A在y轴的正半轴上,点B、C的坐标分别为B(12,8)、C(14,0),AD为⊙E的直径.点M、N分别从A、C两点同时出发做匀速运动,其中点M沿AB向终点B运动,速度为每秒1个单位;点N沿CD向终点D运动,速度为每秒3个单位.当这两点中有一点到达自己的终点时,另一点也停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长交边AD于点F,交CD的延长线于点G.已知DF:FA=1:2.
如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长交边AD于点F,交CD的延长线于点G.已知DF:FA=1:2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
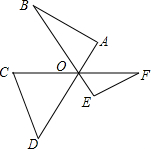 已知线段OA,OB,OC,OD,OE,OF,∠AOB=∠BOC=∠COD=∠DOE=∠EOF=60°,且AD=BE=CF=2,求证:S△OAB+S△OCD+S△OEF<$\sqrt{3}$.
已知线段OA,OB,OC,OD,OE,OF,∠AOB=∠BOC=∠COD=∠DOE=∠EOF=60°,且AD=BE=CF=2,求证:S△OAB+S△OCD+S△OEF<$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com