
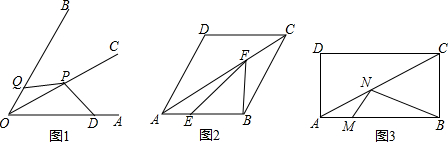
分析 (1)如图1,作D关于直线OC的对称点Q,则DQ的长度就是DP+PQ的最小值,由OC平分∠AOB,∠AOC=30°,得到∠DOQ=60°,于是得到△DOQ是等边三角形,即可得到结果;
(2)由菱形的性质,找出B点关于AC的对称点D,连接DE,则DE就是FE+FB的最小值,再由勾股定理可求出DE;
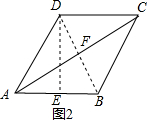
(3)作点B关于AC的对称点B′,过点B′作B′M⊥AB于M,交AC于N,连接AB′交DC于P,连接BM,再根据矩形、轴对称、等腰三角形的性质得出PA=PC,那么在Rt△ADP中,运用勾股定理求出PA的长,然后由cos∠B′AM=cos∠APD,求出AM的长.
解答 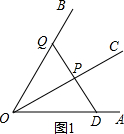 解:(1)如图1,作D关于直线OC的对称点Q,则DQ的长度就是DP+PQ的最小值,
解:(1)如图1,作D关于直线OC的对称点Q,则DQ的长度就是DP+PQ的最小值,
∵OC平分∠AOB,∠AOC=30°,
∴∠DOQ=60°,
∴△DOQ是等边三角形,
∴DQ=OD=10,
∴DP+PQ的最小值是10,
故答案为:10;
(2) 连接DE、BD,
连接DE、BD,
由菱形的对角线互相垂直平分,可得B、D关于AC对称,则FD=FB,
∴FE+FB=EF+FD=DE,
即DE就是FE+FB的最小值,
∵∠BAD=60°,AD=AB,
∴△ABD是等边三角形,
∵AE=BE,
∴DE⊥AB(等腰三角形三线合一的性质),
在Rt△ADE中,DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∴EF+BF的最小值=4$\sqrt{3}$;
(3)如图3,作点B关于AC的对称点B′,过点B′作B′M⊥AB于M,交AC于N,
连接AB′交DC于P,连接BN,
∵四边形ABCD是矩形,
∴DC∥AB,
∴∠BAC=∠PCA,
∵点B关于AC的对称点是B′,
∴∠PAC=∠BAC,
∴∠PAC=∠PCA,
∴PA=PC.
令PA=x,则PC=x,PD=8-x.
在Rt△ADP中,∵PA2=PD2+AD2,
∴x2=(8-x)2+42,
∴x=5,
∵cos∠B′AM=cos∠APD,
∴AM:AB′=DP:AP,
∴AM:8=3:5,
∴AM=$\frac{24}{5}$,
∴B′M=$\sqrt{AB{′}^{2}-A{M}^{2}}$=$\sqrt{{8}^{2}-(\frac{24}{5})^{2}}$=$\frac{32}{5}$,
∴MN+BN的最小值=$\frac{32}{5}$.
点评 本题主要考查了轴对称-最短路线问题,矩形的性质,根据垂线段最短作出辅助线,确定点P,Q,E,F,M、N的位置是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
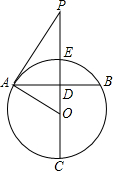 如图,过圆心O的直线PC垂直弦AB于点D,并且与⊙O交于C、E两点.
如图,过圆心O的直线PC垂直弦AB于点D,并且与⊙O交于C、E两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
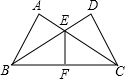 如图,∠A=∠D=90°,AB=DC,AC与BD相交于点E,F是BC的中点.下列说法:①BE=EC;②BF=FC;③EF⊥BC;④∠BEF=∠CEF,正确的有( )个.
如图,∠A=∠D=90°,AB=DC,AC与BD相交于点E,F是BC的中点.下列说法:①BE=EC;②BF=FC;③EF⊥BC;④∠BEF=∠CEF,正确的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
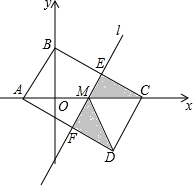 如图,在平面直角坐标系中A(-2,0),B(0,3),C(6,0),D(4,-3),M(2,0),直线l过M点,若S四边形ABCD=mS阴影,求m的值.
如图,在平面直角坐标系中A(-2,0),B(0,3),C(6,0),D(4,-3),M(2,0),直线l过M点,若S四边形ABCD=mS阴影,求m的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com