
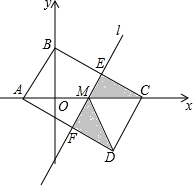
 如图,在平面直角坐标系中A(-2,0),B(0,3),C(6,0),D(4,-3),M(2,0),直线l过M点,若S四边形ABCD=mS阴影,求m的值.
如图,在平面直角坐标系中A(-2,0),B(0,3),C(6,0),D(4,-3),M(2,0),直线l过M点,若S四边形ABCD=mS阴影,求m的值. 分析 首先作DG⊥AC交x轴与点G,判断出DG=3,AM=CM=4,点M是AC的中点;然后判断出BC∥AD,即可判断出△AMF∽△CME,再根据AM=CM,判断出S△CME=S△AMF,据此求出S阴影的值是多少;最后求出四边形ABCD的面积,再根据S四边形ABCD=mS阴影,求出m的值是多少即可.
解答 解:如图1,作DG⊥AC交x轴与点G,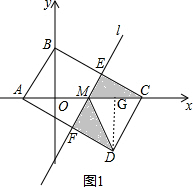 ,
,
∵DG⊥AC,D(4,-3),
∴DG=3,
∵2-(-2)=4,6-2=4,
∴AM=CM=4,点M是AC的中点,
∵${k}_{BC}=\frac{3-0}{0-6}=-\frac{1}{2}$,${k}_{AD}=\frac{0-(-3)}{-2-4}=-\frac{1}{2}$,
∴kBC=kAD,
∴BC∥AD,
∴△AMF∽△CME,
又∵AM=CM,
∴S△CME=S△AMF,
∴S阴影=S△AMF+S△DMF=S△AMD=$\frac{1}{2}AM•DG$=$\frac{1}{2}×4×3=6$;
∵AC=6-(-2)=8,OB=3,DG=3,
∴S四边形ABCD=S△ABC+S△ACD=$\frac{1}{2}×8×3+\frac{1}{2}×8×3=24$,
又∵S四边形ABCD=mS阴影,
∴m=$\frac{{S}_{四边形ABCD}}{{S}_{阴影}}=\frac{24}{6}=4$,
即m的值是4.
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了数形结合思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了三角形相似的判定和性质的应用,以及三角形的面积的求法,要熟练掌握.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
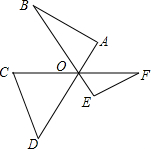 已知线段OA,OB,OC,OD,OE,OF,∠AOB=∠BOC=∠COD=∠DOE=∠EOF=60°,且AD=BE=CF=2,求证:S△OAB+S△OCD+S△OEF<$\sqrt{3}$.
已知线段OA,OB,OC,OD,OE,OF,∠AOB=∠BOC=∠COD=∠DOE=∠EOF=60°,且AD=BE=CF=2,求证:S△OAB+S△OCD+S△OEF<$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (30+x)(100-15x)=3125 | B. | (30-x)(100+15x)=3125 | ||
| C. | (30+x)(100-5x)=3125 | D. | (30-x)(100+5x)=3125 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 交通信号灯有“红、绿、黄”三种颜色,它们发生的概率 | |
| B. | 掷一枚图钉,落地后钉尖“朝上”或“朝下”的概率 | |
| C. | 小亮在沿着“直角三角形”三边的小路上散步,他出现在各边上的概率 | |
| D. | 小明用随机抽签的方式选择以上三种答案,则A、B、C被选中的概率 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com