
【题目】已知矩形OABC中,OA=3,AB=6,以OA、OC所在的直线为坐标轴,建立如图所示的平面直角坐标系。将矩形OABC绕点O顺时针方向旋转,得到矩形ODEF,当点B在直线DE上时,设直线DE和![]() 轴交于点P,与
轴交于点P,与![]() 轴交于点Q.(1)求证:△BCQ≌△ODQ;(2)求点P的坐标;
轴交于点Q.(1)求证:△BCQ≌△ODQ;(2)求点P的坐标;
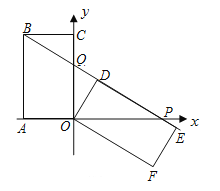
【答案】(1)证明过程见解析;(2)(5,0)
【解析】
试题分析:(1)、根据矩形的性质得出BC=OD,∠BCQ=∠ODQ=90°,结合∠BQC=∠OQD得出三角形全等;(2)、设CQ=x,则BQ=6-x,根据Rt△BCQ求出x的值,从而得出OQ的长度和点Q的坐标,求出直线BQ的解析式,根据解析式得出点P的坐标.
试题解析:(1)、∵矩形![]() 和矩形
和矩形![]() 全等, ∴BC=OD, ∠BCQ=∠ODQ=90°,
全等, ∴BC=OD, ∠BCQ=∠ODQ=90°,
∵∠BQC=∠OQD, ∴△BCQ≌△ODQ.
(2)、∵△BCQ≌△ODQ,∴CQ=DQ,BQ=OQ, 设CQ=x,则OQ=6-x,BQ=6-x,
在Rt△BCQ中,![]() , 解得
, 解得![]() ,
,
∴OQ=![]() ,∴Q(0,
,∴Q(0,![]() ),
),
∵B(-3,6),设BQ:![]() ,依题意得:
,依题意得: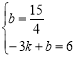 , 解得
, 解得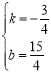 ,
,
∴![]() , 令
, 令![]() ,得
,得![]() , 解得
, 解得![]() ,∴P(5,0).
,∴P(5,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】现定义一种新运算“*”,规定a*b=ab+a﹣b,如1*3=1×3+1﹣3,则(﹣2*5)*6等于( )
A.120
B.125
C.﹣120
D.﹣125
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AD=2㎝,BC=6㎝,AB=7㎝,点P是从点B出发在射线BA上的一个动点,运动的速度是1㎝/s,连结PC、PD.若△PAD与△PBC是相似三角形,则满足条件的点P个数是( )
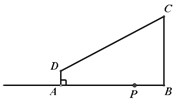
A.5个
B.4个
C.3个
D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个数为三位数,十位数字是a,个位数字比a小2,百位数字是a的2倍,则这个三位数可表示( )
A.21a﹣2
B.211a﹣2
C.200a﹣2
D.3a﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点A(2,4)在函数y=kx﹣2的图象上,则下列各点在此函数图象上的是( )
A. (1,1) B. (﹣1,1) C. (﹣2,﹣2) D. (2,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1所示,在正方形ABCD中,对角线AC与BD相交于点O,请填空:![]() = (直接写出答案);
= (直接写出答案);
(2)如图2所示,将(1)中的△BOC绕点B逆时针旋转得到△BO1C1,连接AO1,DC1,请你猜想线段AO1与DC1之间的数量关系,并证明之;
(3)如图3所示,矩形ABCD和Rt△BEF有公共顶点B,且∠BEF=90°,∠EBF=∠ABD=30°,则![]() 的值是否为定值?若是定值,请求出该值;若不是定值,请简述理由.
的值是否为定值?若是定值,请求出该值;若不是定值,请简述理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算与化简
(1)﹣7+13﹣6+20
(2)23×(﹣5)﹣(﹣3)÷ ![]()
(3)[﹣22﹣(5﹣6)3]÷ ![]() ×
× ![]() ﹣|﹣2|
﹣|﹣2|
(4)﹣(2y﹣5)+(4+3y)
(5)(8xy﹣x2+y2)﹣3(﹣x2+y2+5xy)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车行驶akm后,又以vkm的速度行驶了th,则这辆汽车行驶的全部路程是( )
A. vt B. a+vt C. a-vt D. 2a-vt
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com