
【题目】已知:在四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(![]() )求四边形
)求四边形![]() 的面积.
的面积.
(![]() )点
)点![]() 是线段
是线段![]() 上的动点,连接
上的动点,连接![]() 、
、![]() ,求
,求![]() 周长的最小值及此时
周长的最小值及此时![]() 的长.
的长.

(![]() )点
)点![]() 是线段
是线段![]() 上的动点,
上的动点, ![]() 、
、![]() 为边
为边![]() 上的点,
上的点, ![]() ,连接
,连接![]() 、
、![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,记
,记![]() 和
和![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 的最值.
的最值.

【答案】(![]() )
)![]() .(
.(![]() )
)![]() .3.(
.3.(![]() )
)![]() .
.
【解析】试题分析:(1)如图1,过A作AE⊥BC于E,DF⊥BC于F,得到四边形AEFD是矩形,由矩形的想知道的EF=AD=6,BE=CF=3,根据勾股定理得到![]() ,于是得到结论;
,于是得到结论;
(2)如图2,作点B关于直线AD的对称点G,连接CG交AD于P,则BC+PB+PC=BC+PG+PC即为△BCP周长的最小值,根据勾股定理得到![]() ,于是得到△BCP周长的最小值为:4
,于是得到△BCP周长的最小值为:4![]() +12;根据三角形中位线的性质得到PH=
+12;根据三角形中位线的性质得到PH=![]() BC=6,由勾股定理得到
BC=6,由勾股定理得到![]() ,于是得到结论.
,于是得到结论.
(3)过![]() 点作
点作![]() 的垂线分别交
的垂线分别交![]() 、
、![]() 于
于![]() 、
、![]() 点,过
点,过![]() 点作
点作![]() 的垂线分别交
的垂线分别交![]() 、
、![]() 于
于![]() 、
、![]() 点,过
点,过![]() 点作
点作![]() 的垂线分别交
的垂线分别交![]() 、
、![]() 于
于![]() 、
、![]() 点,如图所示,设
点,如图所示,设![]() ,则
,则![]() .因为
.因为![]() ,所以
,所以![]() ∽
∽![]() ,得
,得![]() ;同理可得
;同理可得![]() ∽
∽![]() ,
, ![]() ∽
∽![]() ,得:
,得: ![]() ,
, ![]() ,所以
,所以![]() ,进而求得答案.
,进而求得答案.
试题解析:(![]() )如图1,过
)如图1,过![]() 作
作![]() 于
于![]() ,
, ![]() 于
于![]() .
.

则四边形![]() 是矩形.
是矩形.
∴![]() ,
, ![]() .
.
∴![]() .
.
∴![]() .
.
(![]() )如图2,作点
)如图2,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,
,

连接![]() 交
交![]() 于
于![]() ,则
,则![]() .
.
即为![]() 的最小周长.
的最小周长.
由(![]() )知
)知![]() .
.
在![]() 中,
中, ![]() .
.
∴![]() 的
的![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
(![]() )过
)过![]() 点作
点作![]() 的垂线分别交
的垂线分别交![]() 、
、![]() 于
于![]() 、
、![]() 点,过
点,过![]() 点作
点作![]() 的垂线分别交
的垂线分别交![]() 、
、![]() 于
于![]() 、
、![]() 点,过
点,过![]() 点作
点作![]() 的垂线分别交
的垂线分别交![]() 、
、![]() 于
于![]() 、
、![]() 点,如图3所示,设
点,如图3所示,设![]() ,则
,则![]() .
.

因为![]() ,所以
,所以![]() ∽
∽![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() ;
;
同理可得![]() ∽
∽![]() ,
, ![]() ∽
∽![]() ,
,
所以![]() ,
, ![]() ,
,
求得: ![]() ,
, ![]() ,其中
,其中![]() ,
,
所以![]() ,
,
即![]()
![]() .
.
因此当![]() 时,
时, ![]() 有最大值
有最大值![]() ;当
;当![]() 或
或![]() 时,
时, ![]() 有最小值了
有最小值了![]() .
.


科目:初中数学 来源: 题型:
【题目】横跨深圳及香港之间的深圳湾大桥(ShenzhenBayBridge)是中国唯一倾斜的独塔单索面桥,大桥全长4 770米,这个数字用科学记数法表示为(保留两个有效数字)( )
A.47×102
B.4.7×103
C.4.8×103
D.5.0×103
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的个数是( )
① 0的平方根是0; ② 1的平方根是1; ③ 0.01是0.1的一个平方根.
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某纺织厂从10万件同类产品中随机抽取100件进行质检,发现其中有5件不合格,那么估计该厂这10万件产品中合格品约有____________万件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D、E分别是△ABC的边BC、AB上的点,△ABC,△BDE,△ACD的周长依次为![]() ,
, ![]() ,
, ![]() .
.
(1)当∠2=∠3,BD=![]() BC时,求
BC时,求![]() 的值;
的值;
(2)当∠1=∠2,BD=![]() BC时,求
BC时,求![]() 的值;
的值;
(3)当∠1=∠2=∠3时,证明: ![]() ≤
≤![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图正比例函数y=2x的图像与一次函数 y=kx+b的图像交于点A(m,2),一次函数的图像经过点B(-2,-1)与y轴交点为C与x轴交点为D.
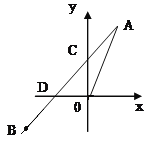
(1)求一次函数的解析式;
(2)求C点的坐标;
(3)求△AOD的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com