
【题目】已知反比例函数的图像与![]() 的图像交于点A、B,A点的坐标是(
的图像交于点A、B,A点的坐标是(![]() ,-2)
,-2)
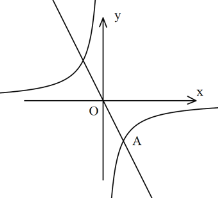
(1)求反比例函数解析式;
(2)求点B的坐标;
(3)在y轴上是否存在点C,使得△ABC的面积是6,若存在,求点C的坐标;若不存在,请说明理由。
【答案】(1)![]() ;(2)(-1,2);(3)(0,6)或(0,-6)
;(2)(-1,2);(3)(0,6)或(0,-6)
【解析】
(1)将点A坐标代入![]() 中,求a的值,然后用待定系数法求反比例函数解析式;(2)根据正比例函数和反比例函数关于原点对称的性质求点B的坐标;(3)设点C的坐标为(0,y),数形结合,根据三角形面积公式列方程求解.
中,求a的值,然后用待定系数法求反比例函数解析式;(2)根据正比例函数和反比例函数关于原点对称的性质求点B的坐标;(3)设点C的坐标为(0,y),数形结合,根据三角形面积公式列方程求解.
解:(1)把A点的坐标(![]() ,-2)代入
,-2)代入![]() 中
中
![]()
解得:a=1
∴A点的坐标是(1,-2)
设反比例函数解析式为:![]()
将A点的坐标(1,-2)代入![]() 中
中
![]()
∴反比例函数的解析式为:![]()
(2)∵正比例函数和反比例函数关于原点对称且它们的图像交于点A、B
∴点A、B关于原点对称
∴B点坐标为:(-1,2)
(3)存在,设点C的坐标为(0,y),连接AC,BC
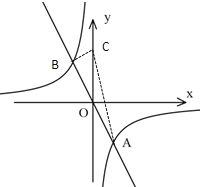
![]()
∴![]()
∴点C的坐标为(0,6)或(0,-6)


科目:初中数学 来源: 题型:
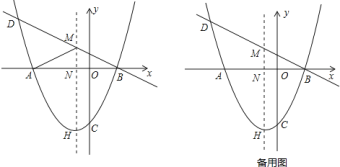
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,顶点为
,顶点为![]() ,其对称轴交
,其对称轴交![]() 轴于点
轴于点![]() .直线
.直线![]() 经过
经过![]() 、
、![]() 两点,交抛物线的对称轴于点
两点,交抛物线的对称轴于点![]() ,其中点
,其中点![]() 的横坐标为
的横坐标为![]() .
.
(1)求抛物线的表达式;
(2)连接![]() ,求
,求![]() 的周长;
的周长;
(3)若![]() 是抛物线位于直线
是抛物线位于直线![]() 的下方且在其对称轴左侧上的一点,当四边形
的下方且在其对称轴左侧上的一点,当四边形![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:①abc<0;②2a﹣b<0;③b2>(a+c)2;④点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2.其中正确的结论有( )
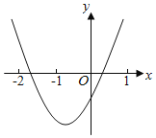
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有![]() 、
、![]() 、
、![]() 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )

A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).

(1)图2中的阴影部分的面积为 ;
(2)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
(3)根据(2)中的结论,若x+y=7,xy=![]() ,则x﹣y= ;
,则x﹣y= ;
(4)实际上通过计算图形的面积可以探求相应的等式.根据图3,写出一个因式分解的等式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲和乙一起做游戏,下列游戏规则对双方公平的是( )

A. 在一个装有2个红球和3个白球(每个球除颜色外都相同)的袋中任意摸出一球,摸到红球甲获胜,摸到白球乙获胜;
B. 从标有号数1到100的100张卡片中,随意抽取一张,抽到号数为奇数甲获胜,否则乙获胜;
C. 任意掷一枚质地均匀的骰子,掷出的点数小于4则甲获胜,掷出的点数大于4则乙获胜;
D. 让小球在如图所示的地板上自由地滚动,并随机地停在某块方块上,若小球停在黑色区域则甲获胜,若停在白色区域则乙获胜
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个盒子中分别装有除颜色外都相同的小球,甲盒中装有两个球,分别为一个红球和一个绿球;乙盒中装有三个球,分别为两个绿球和一个红球;丙盒中装有两个球,分别为一个红球和一个绿球,从三个盒子中各随机取出一个小球
(1)请画树状图,列举所有可能出现的结果
(2)请直接写出事件“取出至少一个红球”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
(1)实践操作:![]() 中,
中,![]() ,
,![]() 为直线
为直线![]() 上一点,过
上一点,过![]() 点作
点作![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,如图①,图②,图③所示,则
,如图①,图②,图③所示,则![]() 的形状为______.
的形状为______.
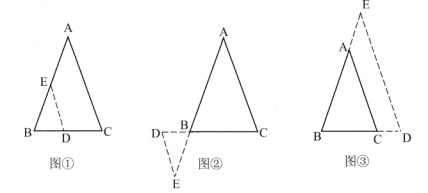
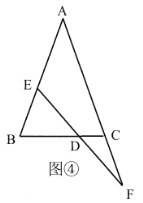
(2)问题解决:等腰三角形是一种特殊的三角形,常与全等三角形的相关知识结合在一起解决问题.如图④,![]() 中,
中,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() ,
,![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() .
.
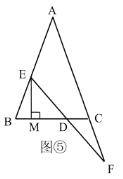
(3)拓展与应用,在(2)的条件下,如图⑤,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,若
,若![]() ,则
,则![]() 的长为______.
的长为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com