
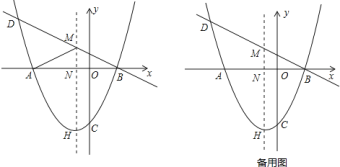
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,顶点为
,顶点为![]() ,其对称轴交
,其对称轴交![]() 轴于点
轴于点![]() .直线
.直线![]() 经过
经过![]() 、
、![]() 两点,交抛物线的对称轴于点
两点,交抛物线的对称轴于点![]() ,其中点
,其中点![]() 的横坐标为
的横坐标为![]() .
.
(1)求抛物线的表达式;
(2)连接![]() ,求
,求![]() 的周长;
的周长;
(3)若![]() 是抛物线位于直线
是抛物线位于直线![]() 的下方且在其对称轴左侧上的一点,当四边形
的下方且在其对称轴左侧上的一点,当四边形![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标.
的坐标.
【答案】(1)抛物线的解析式为![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)将A,B两点的坐标代入抛物线的解析式即可求出.
(2)首先求出D点、A点、B点坐标,进而利用待定系数法求出直线DB的解析式,再利用勾股定理得出BM的长,即可得出△ABM的周长;
(3)首先表示出P,Q点的坐标,进而表示出S四边形DPHM=S△DPM+S△PMH,利用二次函数最值求出即可
![]() 将
将![]() ,
,![]() 点坐标代入解析式,得
点坐标代入解析式,得
![]() ,
,
解得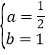 ,
,
抛物线的解析式为![]() ;
;
![]() 当
当![]() ,
,![]() ,则
,则![]() .
.
由![]() ,
,![]() ,
,
则![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
则 ,
,
解得: ,
,
则直线![]() 的解析式为
的解析式为![]() ,
,
抛物线对称轴为![]() ,则
,则![]()
在![]() 中,
中,![]() ,
,
∴![]() ,
,
![]() 垂直平分
垂直平分![]() ,则
,则![]() ,
,
则![]() ,
,
所以![]() 的周长为:
的周长为:![]() ;
;
![]() 如图
如图![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 垂直于
垂直于![]() 轴交
轴交![]() 于
于![]()
抛物线的顶点坐标![]() 为
为![]()
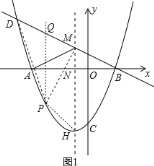
令![]() ,则
,则![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
故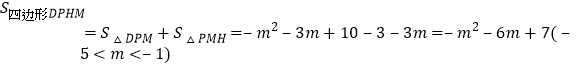
∵![]() ,
,
∴抛物线开口向下,
故当![]() 时,
时,![]() 最大,则
最大,则![]() ,
,
则![]() .
.


科目:初中数学 来源: 题型:
【题目】随着人们环保意识的不断增强,我市家庭电动自行车的拥有量逐年增加.据统计,某小区2009年底拥有家庭电动自行车125辆,2011年底家庭电动自行车的拥有量达到180辆.
(1)若该小区2009年底到2012年底家庭电动自行车拥有量的年平均增长率相同,则该小区到2012年底电动自行车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资3万元再建若干个停车位,据测算,建造费用分别为室内车位1000元/个,露天车位200元/个.考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,则该小区最多可建两种车位各多少个?试写出所有可能的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
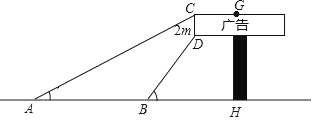
【题目】数学社团小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点在一条直线上,请根据以上数据计算GH的长(![]() =1.73,要求结果精确得到0.1m)
=1.73,要求结果精确得到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图像如图所示,图像过点
的部分图像如图所示,图像过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列结论:(1)
,下列结论:(1)![]() ;(2)
;(2)![]() ;(3)若点
;(3)若点![]() 、点
、点![]() 、点
、点![]() 在该函数图像上,则
在该函数图像上,则![]() ;(4)若方程
;(4)若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() ,则
,则![]() .其中正确结论的序号是________.
.其中正确结论的序号是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年眉山市委市政府积极推进创建“全国文明城市”工作,市创文办公室为了调查中学生对“社会主义核心价值观”内容的了解程度(程度分为:“![]() .非常了解”,“
.非常了解”,“![]() .比较了解”,“
.比较了解”,“![]() .了解较少”,“
.了解较少”,“![]() .不知道”),对我市某中学的学生进行随机抽样调查,根据调查结果绘制了两幅不完整的统计图,请根据图中信息解答下列问题:
.不知道”),对我市某中学的学生进行随机抽样调查,根据调查结果绘制了两幅不完整的统计图,请根据图中信息解答下列问题:
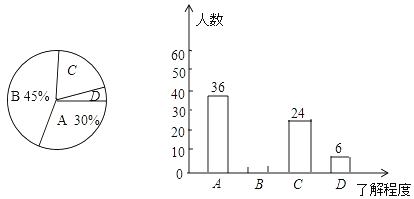
(1)本次抽样调查了多少名学生;
(2)补全条形统计图和扇形统计图;
(3)求扇形统计图中“![]() .了解较少”所在的扇形圆心角的度数;
.了解较少”所在的扇形圆心角的度数;
(4)若该中学共有2600名学生,请你计算这所中学的所有学生中,对“社会主义核心价值观”内容的了解程度为“非常了解”和“比较了解”的学生共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=![]() 的图象上,则k的值为( )
的图象上,则k的值为( )

A.-4 B.4 C.-2 D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
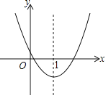
【题目】如图,二次函数![]() 的图象如图所示,则下列说法①
的图象如图所示,则下列说法①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() ;④当
;④当![]() 时,
时,![]() ;⑤关于
;⑤关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根.你认为其中正确的有( )
有两个不相等的实数根.你认为其中正确的有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)当x12+x22=6x1x2时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数的图像与![]() 的图像交于点A、B,A点的坐标是(
的图像交于点A、B,A点的坐标是(![]() ,-2)
,-2)
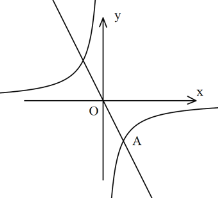
(1)求反比例函数解析式;
(2)求点B的坐标;
(3)在y轴上是否存在点C,使得△ABC的面积是6,若存在,求点C的坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com