
【题目】计算:
(1)(2x2y)3(﹣3xy2)÷6xy
(2)(a+2)2﹣4(a+1)(a﹣1)
(3)|﹣3|+(﹣1)2013×(π﹣3)0﹣(﹣ ![]() )﹣3 .
)﹣3 .
【答案】
(1)解:(2x2y)3(﹣3xy2)÷6xy
=8x6y3(﹣3xy2)÷6xy
=﹣4x6y4
(2)解:(a+2)2﹣4(a+1)(a﹣1)
=a2+4a+4﹣4a2+4
=﹣3a2+4a+8
(3)解:|﹣3|+(﹣1)2013×(π﹣3)0﹣(﹣ ![]() )﹣3
)﹣3
=3+(﹣1)×1﹣(﹣8)
=3﹣1+8
=10.
【解析】(1)根据的积的乘方和同底数幂的乘法和除法可以解答本题;(2)根据完全平方公式和平方差公式可以解答本题;(3)根据绝对值、幂的乘方、零指数幂、负整数指数幂可以解答本题.
【考点精析】关于本题考查的零指数幂法则和整数指数幂的运算性质,需要了解零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数)才能得出正确答案.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于A,B两点(A点在B点的左侧),与y轴交于点C,抛物线的对称轴为x=1.
轴交于A,B两点(A点在B点的左侧),与y轴交于点C,抛物线的对称轴为x=1.
(1)求抛物线的表达式;
(2)若CD∥x轴,点D在点C的左侧, ![]() ,求点D的坐标;
,求点D的坐标;
(3)在(2)的条件下,将抛物线在直线x=t右侧的部分沿直线x=t翻折后的图形记为G,若图形G与线段CD有公共点,请直接写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不讲究说话艺术常引起误会。相传一个人不太会说话,一次他设宴请客,眼看快到中午了,还有几个人没有来,就自言自语地说:“怎么该来的还不来呢?”在座的客人一听,想:难道我们是不该来的?于是有一半人走了,他一看很着急,又说:“嗨,不该走的倒走了!”剩下的人一听,是我们该走啊!于是剩下的又有三分之二的人离开了,他着急的直拍大腿,连说:“我说的不是他们。”结果仅剩下的3个人也都告辞走了。聪明的你知道开始来了多少客人吗?如果设开始来了x位客人,那么所列方程为_ ___(只需列出方程,不解答)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A(﹣3,﹣2)向上平移2个单位,再向右平移2个单位到点B,则点B的坐标为( )
A.(1,0)
B.(1,﹣4)
C.(﹣1,0)
D.(﹣5,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示,∠AOB、∠COD都是直角.
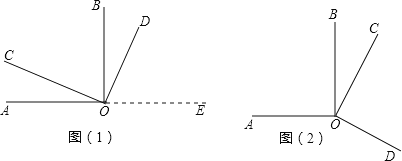
(1)试猜想∠AOD与∠COB在数量上是相等,互余,还是互补的关系.请你用推理的方法说明你的猜想是合理的.
(2)当∠COD绕着点O旋转到图(2)所示位置时,你在(1)中的猜想还成立吗?请你证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=24cm,O为线段AB上一点,且AO:BO=1:2,C、E顺次为射线AB上的动点,点C从A点出发向点B方向运动,E点随之运动,且始终保持CE=8cm(C点到达B点时停止运动),F为OE中点.
(1)当C点运动到AO中点时,求BF长度;
![]()
(2)在C点运动的过程中,猜想线段CF 和BE是否存在特定的数量关系,并说明理由;
![]()
(3)① 当E点运动到B点之后,是否存在常数n,使得OE-n·CF的值不随时间改变而变化.若存在,请求出n和这个不变化的值;若不存在,请说明理由.
![]()
② 若点C的运动速度为2cm/秒,求点C在线段FB上的时间为 秒(直接写出答案);
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com