
【题目】骰子是一种特别的数字立方体(如图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( ).
![]()
A. 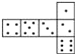 B.
B. 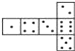 C.
C.  D.
D. 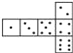
【答案】A
【解析】
正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点对各选项分析判断后利用排除法求解.
根据正方体的表面展开图,相对的面之间一定相隔一个正方形.
A.4点与3点是向对面,5点与2点是向对面,1点与6点是向对面,所以可以折成符合规则的骰子,故本选项正确;
B.1点与3点是向对面,4点与6点是向对面,2点与5点是向对面,所以不可以折成符合规则的骰子,故本选项错误;
C.3点与4点是向对面,1点与5点是向对面,2点与6点是向对面,所以不可以折成符合规则的骰子,故本选项错误;
D.1点与5点是向对面,3点与4点是向对面,2点与6点是向对面,所以不可以折成符合规则的骰子,故本选项错误.
故选A.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:
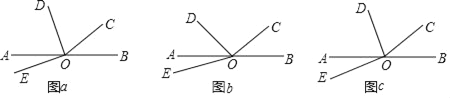
【题目】如图,O为直线AB上一点,∠BOC=α.
(1)若α=40°,OD平分∠AOC,∠DOE=90°,如图(a)所示,求∠AOE的度数;
(2)若∠AOD=![]() ∠AOC,∠DOE=60°,如图(b)所示,请用α表示∠AOE的度数;
∠AOC,∠DOE=60°,如图(b)所示,请用α表示∠AOE的度数;
(3)若∠AOD=![]() ∠AOC,∠DOE=
∠AOC,∠DOE=![]() (n≥2,且n为正整数),如图(c)所示,请用α和n表示∠AOE的度数(直接写出结果).
(n≥2,且n为正整数),如图(c)所示,请用α和n表示∠AOE的度数(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
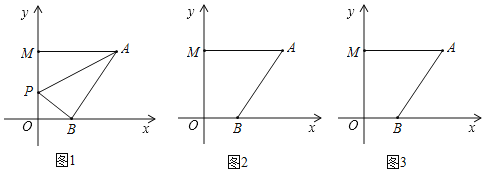
【题目】在平面直角坐标系中,A(6,a),B(b,0),M(0,c),P点为y轴上一动点,且(b﹣2)2+|a﹣6|+![]() =0.
=0.
(1)求点B、M的坐标;
(2)当P点在线段OM上运动时,试问是否存在一个点P使S△PAB=13,若存在,请求出P点的坐标与AB的长度;若不存在,请说明理由.
(3)不论P点运动到直线OM上的任何位置(不包括点O、M),∠PAM、∠APB、∠PBO三者之间是否都存在某种固定的数量关系,如果有,请利用所学知识找出并证明;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 A=3x2+3y2﹣2xy,B=xy﹣2y2﹣2x2.
求:(1)2A﹣3B.
(2)若|2x﹣3|=1,y2=9,|x﹣y|=y﹣x,求 2A﹣3B 的值.
(3)若 x=2,y=﹣4 时,代数式 ax3![]() by+5=17,那么当 x=﹣4,y=﹣
by+5=17,那么当 x=﹣4,y=﹣![]() 时,求代 数式 3ax﹣24by3+6 的值.
时,求代 数式 3ax﹣24by3+6 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个几何体由几个大小相同的小立方块搭成,从正面和上面观察这 个几何体,看到的形状都一样(如图所示).
(1)这个几何体最少有多少个小立方块,最多有多少个小立方块;
(2)当摆放的小立方块最多时,请画出从左面观察到的视图.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
①abc<0;②a(b+c)>0;③a﹣c=b;④![]() .
.
![]()
其中正确的个数有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c与x轴只有一个交点,且图象过A(x1 , m)、B(x1+n,m)两点,则m、n的关系为( )
A.m= ![]() n
n
B.m= ![]() n
n
C.m= ![]()
![]()
D.m= ![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知正方形的边长为4,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的3倍,则它们第2018次相遇在边 ( )上.
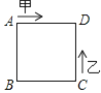
A. AB B. BC C. CD D. DA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB(结果保留根号)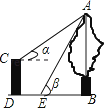
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com