
【题目】如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB(结果保留根号)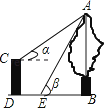
【答案】解:作CF⊥AB于点F,设AF=x米,
在Rt△ACF中,tan∠ACF= ![]() ,
,
则CF= ![]() =
= ![]() x,
x,
在直角△ABE中,AB=x+BF=4+x(米),
在直角△ABF中,tan∠AEB= ![]() ,则BE=
,则BE= ![]() =
= ![]() (x+4)米.
(x+4)米.
∵CF﹣BE=DE,即 ![]() x﹣
x﹣ ![]() (x+4)=3.
(x+4)=3.
解得:x= ![]() ,
,
则AB= ![]() +4=
+4= ![]() (米).
(米).
答:树高AB是 ![]() 米.
米.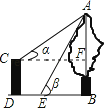
【解析】作CF⊥AB于点F,设AF=x米,在直角△ACF中利用三角函数用x表示出CF的长,在直角△ABE中表示出BE的长,然后根据CF﹣BE=DE即可列方程求得x的值,进而求得AB的长.本题考查了解直角三角形的应用,解答本题关键是构造直角三角形,利用三角函数的知识表示出相关线段的长度.
【考点精析】掌握关于仰角俯角问题是解答本题的根本,需要知道仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】骰子是一种特别的数字立方体(如图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( ).
![]()
A. 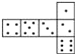 B.
B. 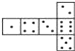 C.
C.  D.
D. 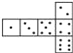
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B′处.求:
x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B′处.求:
(1)点B′的坐标;
(2)直线AM所对应的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,△ABC是等腰直角三角形,∠BAC=90°,DE是经过点A的直线,作BD⊥DE,CE⊥DE,
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,我们能得到什么结论?并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年“母亲节”前夕,宜宾某花店用4000元购进若干束花,很快售完,接着又用4500元购进第二批花,已知第二批所购花的束数是第一批所购花束数的1.5倍,且每束花的进价比第一批的进价少5元
(1)求第一批花每束的进价是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,延长△ABC的各边,使得BF=AC,AE=CD=AB,连结DE,EF,FD,得到△DEF为等边三角形.
求证:(1)△AEF≌△CDE;
(2)△ABC为等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列因式分解,正确的是( )
A. x2y2-z2=x2(y+z)(y-z) B. -x2y+4xy-5y=-y(x2+4x+5)
C. (x+2)2-9=(x+5)(x-1) D. 9-12a+4a2=-(3-2a)2
【答案】C
【解析】解析:选项A.用平方差公式法,应为x2y2-z2=(xy+z)·(xy-z),故本选项错误.
选项B.用提公因式法,应为-x2y+ 4xy-5y=- y(x2- 4x+5),故本选项错误.
选项C.用平方差公式法,(x+2)2-9=(x+2+3)(x+2-3)=(x+5)(x-1),故本选项正确.
选项D.用完全平方公式法,应为9-12a+4a2=(3-2a)2,故本选项错误.
故选C.
点睛:(1)完全平方公式: ![]() .
.
(2)平方差公式:(a+b)(a-b)= ![]() .
.
(3)常用等价变形: ![]()
![]() ,
,
![]() ,
,
![]() .
.
【题型】单选题
【结束】
10
【题目】已知a,b,c分别是△ABC的三边长,且满足2a4+2b4+c4=2a2c2+2b2c2,则△ABC是( )
A. 等腰三角形 B. 等腰直角三角形
C. 直角三角形 D. 等腰三角形或直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数y= ![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3,
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3, 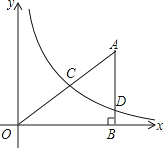
(1)求反比例函数y= ![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com