
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数y= ![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3,
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3, 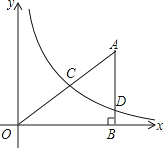
(1)求反比例函数y= ![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
【答案】
(1)
解:设点D的坐标为(4,m)(m>0),则点A的坐标为(4,3+m),
∵点C为线段AO的中点,
∴点C的坐标为(2, ![]() ).
).
∵点C、点D均在反比例函数y= ![]() 的函数图象上,
的函数图象上,
∴ 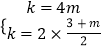 ,解得:
,解得: ![]() .
.
∴反比例函数的解析式为y= ![]()
(2)
解:∵m=1,
∴点A的坐标为(4,4),
∴OB=4,AB=4.
在Rt△ABO中,OB=4,AB=4,∠ABO=90°,
∴OA= ![]() =4
=4 ![]() ,cos∠OAB=
,cos∠OAB= ![]() =
= ![]()
(3)
解:∵m=1,
∴点C的坐标为(2,2),点D的坐标为(4,1).
设经过点C、D的一次函数的解析式为y=ax+b,
则有 ![]() ,解得:
,解得: 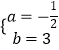 .
.
∴经过C、D两点的一次函数解析式为y=﹣ ![]() x+3
x+3
【解析】(1)设点D的坐标为(4,m)(m>0),则点A的坐标为(4,3+m),由点A的坐标表示出点C的坐标,根据C、D点在反比例函数图象上结合反比例函数图象上点的坐标特征即可得出关于k、m的二元一次方程,解方程即可得出结论;(2)由m的值,可找出点A的坐标,由此即可得出线段OB、AB的长度,通过解直角三角形即可得出结论;(3)由m的值,可找出点C、D的坐标,设出过点C、D的一次函数的解析式为y=ax+b,由点C、D的坐标利用待定系数法即可得出结论.本题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征、解直角三角形以及待定系数法求函数解析式,解题的关键是(1)由反比例函数图象上点的坐标特征找出关于k、m的二元一次方程组(2)求出点A的坐标;(2)求出点C、D的坐标.本题属于基础题,难度不大,但考查的知识点较多,解决该题型题目时,利用反比例函数图象上点的坐标特征找出方程组,通过解方程组得出点的坐标,再利用待定系数法求出函数解析式即可.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】如图:已知正方形的边长为4,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的3倍,则它们第2018次相遇在边 ( )上.
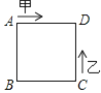
A. AB B. BC C. CD D. DA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB(结果保留根号)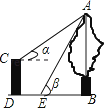
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分,而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了,有一种用“因式分解”法产生的密码、方便记忆,其原理是:将一个多项式分解因式,如多项式:![]() 因式分解的结果为
因式分解的结果为![]() ,当
,当![]() 时,
时,![]() 此时可以得到数字密码171920.
此时可以得到数字密码171920.
(1)根据上述方法,当![]() 时,对于多项式
时,对于多项式![]() 分解因式后可以形成哪些数字密码?(写出三个)
分解因式后可以形成哪些数字密码?(写出三个)
(2)若一个直角三角形的周长是24,斜边长为10,其中两条直角边分别为x、y,求出一个由多项式![]() 分解因式后得到的密码(只需一个即可);
分解因式后得到的密码(只需一个即可);
(3)若多项式![]() 因式分解后,利用本题的方法,当
因式分解后,利用本题的方法,当![]() 时可以得到其中一个密码为242834,求m、n的值.
时可以得到其中一个密码为242834,求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,则a,b满足的关系是

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E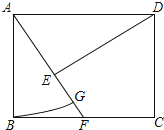
(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为() 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上,A、B两点表示的数a,b满足|a﹣6|+(b+12)2=0
(1)a= ,b= ;
(2)若小球M从A点向负半轴运动、小球N从B点向正半轴运动,两球同时出发,小球M运动的速度为每秒2个单位,当M运动到OB的中点时,N点也同时运动到OA的中点,则小球N的速度是每秒 个单位;
(3)若小球M、N保持(2)中的速度,分别从A、B两点同时出发,经过 秒后两个小球相距两个单位长度.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com