
【题目】在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分,而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了,有一种用“因式分解”法产生的密码、方便记忆,其原理是:将一个多项式分解因式,如多项式:![]() 因式分解的结果为
因式分解的结果为![]() ,当
,当![]() 时,
时,![]() 此时可以得到数字密码171920.
此时可以得到数字密码171920.
(1)根据上述方法,当![]() 时,对于多项式
时,对于多项式![]() 分解因式后可以形成哪些数字密码?(写出三个)
分解因式后可以形成哪些数字密码?(写出三个)
(2)若一个直角三角形的周长是24,斜边长为10,其中两条直角边分别为x、y,求出一个由多项式![]() 分解因式后得到的密码(只需一个即可);
分解因式后得到的密码(只需一个即可);
(3)若多项式![]() 因式分解后,利用本题的方法,当
因式分解后,利用本题的方法,当![]() 时可以得到其中一个密码为242834,求m、n的值.
时可以得到其中一个密码为242834,求m、n的值.
【答案】(1)211428;,212814,142128;(2)48100;(3)m、n的值分别是56、17
【解析】试题分析:(1)先分解因式得到x3-xy2=x(x-y)(x+y),然后利用题中设计密码的方法写出所有可能的密码;
(2)利用勾股定理和周长得到x+y=14,x2+y2=100,再利用完全平方公式可计算出xy=48,然后与(1)小题的解决方法一样;
(3)由x=27时可以得到其中一个密码为242834,可得x3+(m-3n)x2-nx-21因式分解为(x-3)(x+1)(x+7),再利用多项式的乘法法则展开,然后与x3+(m-3n)x2-nx-21比较,即可求出m、n的值.
试题解析:(1)x3-xy2=x(x-y)(x+y),
当x=21,y=7时,x-y=14,x+y=28,
可得数字密码是211428,也可以是212814,142128;
(2)由题意得:![]() ,
,
解得![]() ,
,
而![]() ,
,
所以可得数字密码为48100;
(3)由题意得![]() ,
,
![]() ,
,
![]() ,
,
![]() ,解得
,解得![]() ,
,
故m、n的值分别是56、17.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案科目:初中数学 来源: 题型:
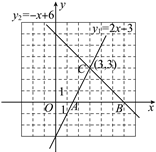
【题目】已知一次函数y1=2x-3,y2=-x+6在同一直角坐标系中的图象如图所示,它们的交点坐标为C(3,3).
(1)根据图象指出x为何值时,y1>y2;x为何值时,y1<y2.
(2)求这两条直线与x轴所围成的△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,△ABC是等腰直角三角形,∠BAC=90°,DE是经过点A的直线,作BD⊥DE,CE⊥DE,
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,我们能得到什么结论?并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,延长△ABC的各边,使得BF=AC,AE=CD=AB,连结DE,EF,FD,得到△DEF为等边三角形.
求证:(1)△AEF≌△CDE;
(2)△ABC为等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列因式分解,正确的是( )
A. x2y2-z2=x2(y+z)(y-z) B. -x2y+4xy-5y=-y(x2+4x+5)
C. (x+2)2-9=(x+5)(x-1) D. 9-12a+4a2=-(3-2a)2
【答案】C
【解析】解析:选项A.用平方差公式法,应为x2y2-z2=(xy+z)·(xy-z),故本选项错误.
选项B.用提公因式法,应为-x2y+ 4xy-5y=- y(x2- 4x+5),故本选项错误.
选项C.用平方差公式法,(x+2)2-9=(x+2+3)(x+2-3)=(x+5)(x-1),故本选项正确.
选项D.用完全平方公式法,应为9-12a+4a2=(3-2a)2,故本选项错误.
故选C.
点睛:(1)完全平方公式: ![]() .
.
(2)平方差公式:(a+b)(a-b)= ![]() .
.
(3)常用等价变形: ![]()
![]() ,
,
![]() ,
,
![]() .
.
【题型】单选题
【结束】
10
【题目】已知a,b,c分别是△ABC的三边长,且满足2a4+2b4+c4=2a2c2+2b2c2,则△ABC是( )
A. 等腰三角形 B. 等腰直角三角形
C. 直角三角形 D. 等腰三角形或直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校共有5个大餐厅和2个小餐厅。经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐。
(1)1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数y= ![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3,
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3, 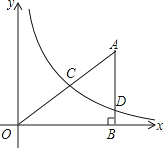
(1)求反比例函数y= ![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题

(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定: 这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景)如图(a),△ABC与△ADE均是顶角为40°的等腰三角形,BC,DE分别是底边,求证:BD=CE.
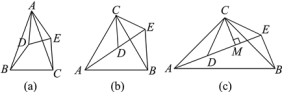
(探究)如图(b),△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
①∠AEB的度数为________;②线段BE与AD之间的数量关系是________.
(拓展)如图(c),△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.
①求∠AEB的度数;
②请直接写出线段CM,AE,BE之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com