
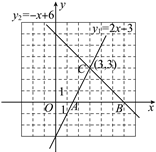
【题目】已知一次函数y1=2x-3,y2=-x+6在同一直角坐标系中的图象如图所示,它们的交点坐标为C(3,3).
(1)根据图象指出x为何值时,y1>y2;x为何值时,y1<y2.
(2)求这两条直线与x轴所围成的△ABC的面积.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知:如图数轴上两点A、B所别应的分别为﹣3、1,点P在数轴上从点A出发以每秒钟2个单位的长度的速度向右运动,点Q在数轴上从点B出发以每秒钟1个单位长度的速度向左运动,设点P的运动时间为t秒.
(1)直接写出线段AB的中点所对应的数及t秒后点P所对应的数.
(2)若点P和点Q同时出发,求点P和点Q相遇时的位置所对应的数;
(3)若点P比点Q迟1秒钟出发,问点P出发几秒后,点P和点Q刚好相距1个单位长度.并问此时数轴上是否存在一个点C,使其到点A、点P和点Q这三点的距离和最小?若存在,直接写出点C所对应的数;若不存在,试说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 A=3x2+3y2﹣2xy,B=xy﹣2y2﹣2x2.
求:(1)2A﹣3B.
(2)若|2x﹣3|=1,y2=9,|x﹣y|=y﹣x,求 2A﹣3B 的值.
(3)若 x=2,y=﹣4 时,代数式 ax3![]() by+5=17,那么当 x=﹣4,y=﹣
by+5=17,那么当 x=﹣4,y=﹣![]() 时,求代 数式 3ax﹣24by3+6 的值.
时,求代 数式 3ax﹣24by3+6 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
①abc<0;②a(b+c)>0;③a﹣c=b;④![]() .
.
![]()
其中正确的个数有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c与x轴只有一个交点,且图象过A(x1 , m)、B(x1+n,m)两点,则m、n的关系为( )
A.m= ![]() n
n
B.m= ![]() n
n
C.m= ![]()
![]()
D.m= ![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型企业为了保护环境,准备购买A、B两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购买A型2台、B型3台需54万,购买A型4台、B型2台需68万元.
(1)求出A型、B型污水处理设备的单价;
(2)经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1565吨,请你为该企业设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知正方形的边长为4,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的3倍,则它们第2018次相遇在边 ( )上.
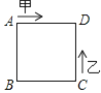
A. AB B. BC C. CD D. DA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( ) 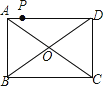
A.4.8
B.5
C.6
D.7.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分,而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了,有一种用“因式分解”法产生的密码、方便记忆,其原理是:将一个多项式分解因式,如多项式:![]() 因式分解的结果为
因式分解的结果为![]() ,当
,当![]() 时,
时,![]() 此时可以得到数字密码171920.
此时可以得到数字密码171920.
(1)根据上述方法,当![]() 时,对于多项式
时,对于多项式![]() 分解因式后可以形成哪些数字密码?(写出三个)
分解因式后可以形成哪些数字密码?(写出三个)
(2)若一个直角三角形的周长是24,斜边长为10,其中两条直角边分别为x、y,求出一个由多项式![]() 分解因式后得到的密码(只需一个即可);
分解因式后得到的密码(只需一个即可);
(3)若多项式![]() 因式分解后,利用本题的方法,当
因式分解后,利用本题的方法,当![]() 时可以得到其中一个密码为242834,求m、n的值.
时可以得到其中一个密码为242834,求m、n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com