
【题目】如图:已知正方形的边长为4,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的3倍,则它们第2018次相遇在边 ( )上.
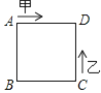
A. AB B. BC C. CD D. DA
【答案】C
【解析】
根据甲、乙移动情况,探究甲、乙相遇所在边的规律,即可得出甲、乙第1次相遇在边CD上、第2次相遇在边AD上、第3次相遇在边AB上、…,由此即可得出甲、乙相遇位置每四次一循环,再根据2018=504×4+2即可得出甲、乙第2018次相遇在边AD上.
解:正方形的边长为4,因为乙的速度是甲的速度的3倍,时间相同,甲乙所行的路程比为1:3,把正方形的每一条边平均分成2份,由题意知:
①第一次相遇甲乙行的路程和为8,甲行的路程为![]() ,乙行的路程为8-2=6,在AD边相遇;
,乙行的路程为8-2=6,在AD边相遇;
②第二次相遇甲乙行的路程和为16,甲行的路程为![]() ,乙行的路程为16-4=12,在DC边相遇;
,乙行的路程为16-4=12,在DC边相遇;
③第三次相遇甲乙行的路程和为16,甲行的路程为![]() ,乙行的路程为16-4=12,在CB边相遇;
,乙行的路程为16-4=12,在CB边相遇;
④第四次相遇甲乙行的路程和为16,甲行的路程为![]() ,乙行的路程为16-4=12,在AB边相遇;
,乙行的路程为16-4=12,在AB边相遇;
……
∴甲、乙相遇位置每四次为一个循环周期.可列表如下:
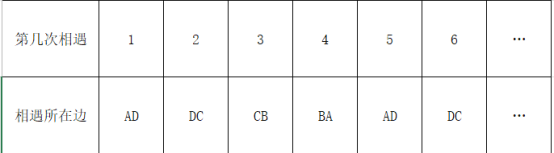
![]()
![]()
故选:C.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
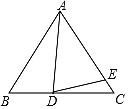
【题目】如图所示,已知在△ABC中,AB=AC,D为线段BC上一点,E为线段AC上一点,且AD=AE.
(1)若∠ABC=60°,∠ADE=70°,求∠BAD与∠CDE的度数;
(2)设∠BAD=α,∠CDE=β,试写出α、β之间的关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骰子是一种特别的数字立方体(如图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( ).
![]()
A. 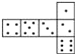 B.
B. 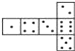 C.
C.  D.
D. 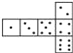
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y1=2x-3,y2=-x+6在同一直角坐标系中的图象如图所示,它们的交点坐标为C(3,3).
(1)根据图象指出x为何值时,y1>y2;x为何值时,y1<y2.
(2)求这两条直线与x轴所围成的△ABC的面积.
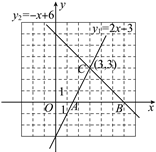
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连结BD.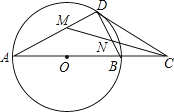
(1)求证:∠A=∠BDC;
(2)若CM平分∠ACD,且分别交AD、BD于点M、N,当DM=1时,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“古诗送郎从军:送郎一路雨飞池,十里江亭折柳枝;离人远影疾行去,归来梦醒度相思.”中,如果用纵轴y表示从军者与送别者行进中离原地的距离,用横轴x表示送别进行的时间,从军者的图象为O→A→B→C,送别者的图象为O→A→B→D,那么下面的图象与上述诗的含义大致吻合的是( )
A. 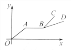 B.
B. 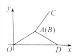 C.
C. 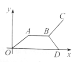 D.
D. 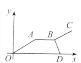
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B′处.求:
x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B′处.求:
(1)点B′的坐标;
(2)直线AM所对应的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,△ABC是等腰直角三角形,∠BAC=90°,DE是经过点A的直线,作BD⊥DE,CE⊥DE,
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,我们能得到什么结论?并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数y= ![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3,
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3, 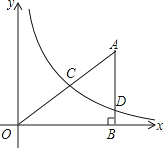
(1)求反比例函数y= ![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com