练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】将6张小长方形纸片（如图1所示）按图2所示的方式不重叠的放在长方形ABCD内，未被覆盖的部分恰好分割为两个长方形，面积分别为S1和S2．已知小长方形纸片的长为a，宽为b，且a>b．当AB长度不变而BC变长时，将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内，S1与S2的差总保持不变，则a，b满足的关系是

    A. B.

    C. D.

    【答案】D

    【解析】

    表示出左上角与右下角部分的面积，求出它们的差，根据它们的差与BC无关即可求出a与b的关系式．

    设S1的长为x，则宽为4b，S2的长为y，则宽为a，
    则AB=4b+a，BC=y+2b，
    ∵x+a=y+2b，
    ∴y-x=a-2b，
    S1与S2的差=ay-4bx=ay-4b（y-a+2b）=（a-4b）y+4ab-8b2，
    ∴a-4b=0，
    即b=a．
    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，将矩形ABCD沿GH对折，点C落在Q处，点D落在AB边上的E处，EQ与BC相交于点F，若AD=8，AE=4，则△EBF周长的大小为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】边长为4cm的正方形ABCD绕它的顶点A旋转180°，顶点B所经过的路线长为 cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】适合下列条件的△ABC中，直角三角形的个数为（　　）

    ①a=3，b=4，c=5； ②a=6，∠A=45°；③a=2，b=2，c=2； ④∠A=38°，∠B=52°．

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①有一个宝塔，它的地基边缘是周长为26m的正五边形ABCDE（如图②），点O为中心．（下列各题结果精确到0.1m）

    （1）求地基的中心到边缘的距离；
    （2）己知塔的墙体宽为1m，现要在塔的底层中心建一圆形底座的塑像，并且留出最窄处为1.6m的观光通道，问塑像底座的半径最大是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

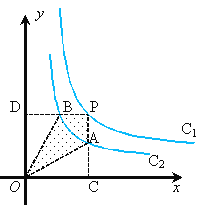
    【题目】如图，两个反比例函数C1:y=和C2:y=在第一象限内的图象如图，P在C1上作PC、PD垂直于坐标轴，垂线与C2交点为A、B，则下列结论，其中正确的是( )

    ①△ODB与△OCA的面积相等；②四边形PAOB的面积等于k1- k2；③PA与PB始终相等；④当点A是PC的中点时，点B一定是PD的中点

    A. ①② B. ②④ C. ①②④ D. ①③④

    【答案】C

    【解析】①∵A、B两点都在y=上，∴△ODB与△OCA的面积都都等于，则①正确；②S矩形OCPB-S△AOC-S△DBO=|k2|-2×|k1|÷2=k2-k1，则②正确；③只有当P的横纵坐标相等时，PA=PB，错误；④当点A是PC的中点时，点B一定是PD的中点，正确．故选C．

    【题型】单选题
    【结束】
    10

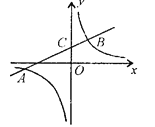
    【题目】如图，反比例函数（k＞0）与一次函数的图象相交于两点A(,),B(,),线段AB交y轴与C，当|－ |=2且AC = 2BC时，k、b的值分别为（ ）

    A. k＝,b＝2 B. k＝,b＝1 C. k＝,b＝ D. k＝,b＝

    查看答案和解析>>

    科目：初中数学 来源： 题型：

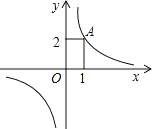
    【题目】如上图，反比例函数的图象位于第一、三象限，其中第一象限内的图象经过点A（1，2），请在第三象限内的图象上找一个你喜欢的点P，你选择的P点坐标为　　　　．

    【答案】（-1，-2）（答案不唯一）．

    【解析】试题分析：根据“第一象限内的图象经过点A（1，2）”先求出函数解析式，给x一个值负数，求出y值即可得到坐标．

    试题解析：∵图象经过点A（1，2），

    ∴

    解得k=2，

    ∴函数解析式为y=，

    当x=-1时，y==-2，

    ∴P点坐标为（-1，-2）（答案不唯一）．

    考点：反比例函数图象上点的坐标特征．

    【题型】填空题
    【结束】
    13

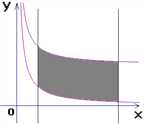
    【题目】在y轴右侧且平行于y轴的直线l被反比例函数（）与函数（）所截，当直线l向右平移4个单位时，直线l被两函数图象所截得的线段扫过的面积为__________平方单位．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知y是x的反比例函数，且当x=-4时，y=,

    （1）求这个反比例函数关系式和自变量x的取值范围；

    （2）求当x=6时函数y的值.

    【答案】（1） （2）

    【解析】整体分析：

    （1）由反比例函数的这定义求k值，确定x的取值范围；（2）把x=6代入（1）中求得的反比例函数的解析式.

    解：（1）设反比例函数关系式为，

    则k=-4×=-2，

    所以个反比例函数关系式是，自变量x的取值范围是x≠0.

    （2）当x=6时， ==-.

    【题型】解答题
    【结束】
    18

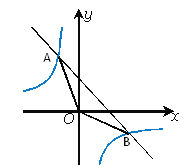
    【题目】如图，函数y= 和y= - x+4的图像交点为A、B，原点为O，求△AOB面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】D、E分别是不等边三角形ABC（即AB≠BC≠AC）的边AB、AC的中点．O是△ABC所在平面上的动点，连接OB、OC，点G、F分别是OB、OC的中点，顺次连接点D、G、F、E．

    （1）如图，当点O在△ABC的内部时，求证：四边形DGFE是平行四边形；

    （2）若四边形DGFE是菱形，则OA与BC应满足怎样的数量关系？（直接写出答案，不需要说明理由．）

    查看答案和解析>>

    同步练习册答案