
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E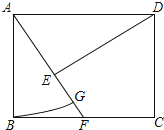
(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)
【答案】
(1)
证明:∵四边形ABCD是矩形,
∴∠B=90°,AD=BC,AD∥BC,
∴∠DAE=∠AFB,
∵DE⊥AF,
∴∠AED=90°=∠B,
在△ABF和△DEA中
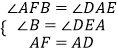 ,
,
∴△ABF≌△DEA(AAS),
∴DE=AB;
(2)
解:∵BC=AD,AD=AF,
∴BC=AF,
∵BF=1,∠ABF=90°,
∴由勾股定理得:AB= ![]() =
= ![]() ,
,
∴∠BAF=30°,
∵△ABF≌△DEA,
∴∠GDE=∠BAF=30°,DE=AB=DG= ![]() ,
,
∴扇形ABG的面积= ![]() =
= ![]() π.
π.
【解析】(1)根据矩形的性质得出∠B=90°,AD=BC,AD∥BC,求出∠DAE=∠AFB,∠AED=90°=∠B,根据AAS推出△ABF≌△DEA即可;
(2)根据勾股定理求出AB,解直角三角形求出∠BAF,根据全等三角形的性质得出DE=DG=AB= ![]() ,∠GDE=∠BAF=30°,根据扇形的面积公式求出即可.本题考查了弧长公式,全等三角形的性质和判定,解直角三角形,勾股定理,矩形的性质的应用,能综合运用性质进行推理和计算是解此题的关键.
,∠GDE=∠BAF=30°,根据扇形的面积公式求出即可.本题考查了弧长公式,全等三角形的性质和判定,解直角三角形,勾股定理,矩形的性质的应用,能综合运用性质进行推理和计算是解此题的关键.
【考点精析】通过灵活运用矩形的性质和扇形面积计算公式,掌握矩形的四个角都是直角,矩形的对角线相等;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)即可以解答此题.


科目:初中数学 来源: 题型:
【题目】“古诗送郎从军:送郎一路雨飞池,十里江亭折柳枝;离人远影疾行去,归来梦醒度相思.”中,如果用纵轴y表示从军者与送别者行进中离原地的距离,用横轴x表示送别进行的时间,从军者的图象为O→A→B→C,送别者的图象为O→A→B→D,那么下面的图象与上述诗的含义大致吻合的是( )
A. 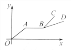 B.
B. 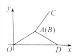 C.
C. 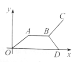 D.
D. 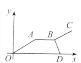
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,延长△ABC的各边,使得BF=AC,AE=CD=AB,连结DE,EF,FD,得到△DEF为等边三角形.
求证:(1)△AEF≌△CDE;
(2)△ABC为等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校共有5个大餐厅和2个小餐厅。经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐。
(1)1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数y= ![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3,
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3, 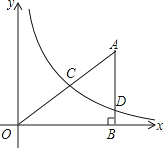
(1)求反比例函数y= ![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题

(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定: 这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次综合实践活动中,小明要测某地一座古塔AE的高度.如图,已知塔基顶端B(和A、E共线)与地面C处固定的绳索的长BC为80m.她先测得∠BCA=35°,然后从C点沿AC方向走30m到达D点,又测得塔顶E的仰角为50°,求塔高AE.(人的高度忽略不计,结果用含非特殊角的三角函数表示)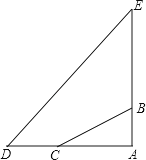
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com