【题目】在一次综合实践活动中，小明要测某地一座古塔AE的高度．如图，已知塔基顶端B（和A、E共线）与地面C处固定的绳索的长BC为80m．她先测得∠BCA=35°，然后从C点沿AC方向走30m到达D点，又测得塔顶E的仰角为50°，求塔高AE．（人的高度忽略不计，结果用含非特殊角的三角函数表示）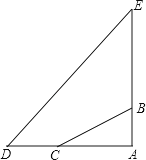
【答案】解：在Rt△ABC中，∠ACB=35°，BC=80m，
∴cos∠ACB= 
，
∴AC=80cos35°，
在Rt△ADE中，tan∠ADE= 
，
∵AD=AC+DC=80cos35°+30，
∴AE=（80cos35°+30）tan50°．
答：塔高AE为（80cos35°+30）tan50°m
【解析】根据锐角三角函数关系，得出cos∠ACB= ，得出AC的长即可；利用锐角三角函数关系，得出tan∠ADE= ，求出AE即可．此题主要考查了解直角三角形的应用，根据已知正确得出锐角三角函数关系是解题关键．
【考点精析】利用关于仰角俯角问题对题目进行判断即可得到答案，需要熟知仰角：视线在水平线上方的角；俯角：视线在水平线下方的角．
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，点F在边BC上，且AF=AD，过点D作DE⊥AF，垂足为点E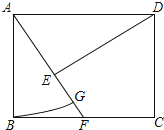
（1）求证：DE=AB；
（2）以A为圆心，AB长为半径作圆弧交AF于点G，若BF=FC=1，求扇形ABG的面积．（结果保留π）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，
(1)求证：四边形ADCE为矩形；
(2)当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在下列解题过程的空白处填上适当的内容（推理的理由或数学表达式）
如图，在△ABC中，已知∠ADE＝∠B，∠1＝∠2，FG⊥AB于点G.
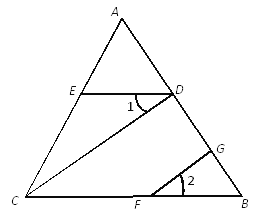
求证CD⊥AB.
证明:∵∠ADE＝∠B（已知），
∴ （ ），
∵ DE∥BC（已证），
∴ （ ），
又∵∠1＝∠2（已知），
∴ （ ），
∴CD∥FG（ ），
∴ （两直线平行同位角相等），
∵ FG⊥AB（已知），
∴∠FGB＝90°（垂直的定义）.
即∠CDB＝∠FGB＝90°，
∴CD⊥AB. （垂直的定义）.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
