练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AB∥CD，直线EF分别交AB，CD于点E，F，∠BEF的平分线与∠DFE的平分线相交于点P，试说明△EPF为直角三角形.

    【答案】证明见解析

    【解析】试题分析：由AB∥CD，可知∠BEF与∠DFE互补，由角平分线的性质可得∠PEF+∠PFE=90°，由三角形内角和定理可得∠P=90°，即可判定△EPF为直角三角形.．

    试题解析：

    ∵AB∥CD,

    ∴∠BEF+∠DFE=180°.

    ∵EP为∠BEF的平分线，FP为∠EFD的平分线，

    ∴∠PEF=∠BEF,∠PFE=∠DFE.

    ∴∠PFE+∠PEF= (∠BEF+∠DFE)= ×180°=90°.

    ∴∠EPF=180°-(∠PEF+∠PFE)=90°.

    ∴△EFP为直角三角形.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=x2+bx+c与x轴交于A、B两点，B点坐标为（3，0），与y轴交于点C（0，﹣3）
    （1）求抛物线的解析式；
    （2）点P在抛物线位于第四象限的部分上运动，当四边形ABPC的面积最大时，求点P的坐标和四边形ABPC的最大面积．
    （3）直线l经过A、C两点，点Q在抛物线位于y轴左侧的部分上运动，直线m经过点B和点Q，是否存在直线m，使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似？若存在，求出直线m的解析式，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

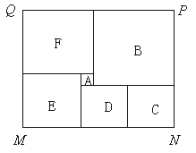
    【题目】如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.

    （1）若设图中最大正方形B的边长是x米,请用含x的代数式分别表示出：

    正方形F的边长= 米;正方形E的边长= 米;正方形C的边长= 米;

    （2）观察图形的特点可知,长方形相对的两边是相等的（如图中的MN=PQ）.根据等量关系可求出x= ;

    （3）现沿着长方形广场的四条边铺设下水管道,由甲、乙2个工程队单独铺设分别需要10天、15天完成.如果两队从同一点开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,试问乙还要多少天完成?甲、乙2个工程队各铺设多少米?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知平行四边形ABCD的顶点A在第三象限，对角线AC的中点在坐标原点，一边AB与x轴平行且AB=2，若点A的坐标为（a，b），则点D的坐标为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一次综合实践活动中，小明要测某地一座古塔AE的高度．如图，已知塔基顶端B（和A、E共线）与地面C处固定的绳索的长BC为80m．她先测得∠BCA=35°，然后从C点沿AC方向走30m到达D点，又测得塔顶E的仰角为50°，求塔高AE．（人的高度忽略不计，结果用含非特殊角的三角函数表示）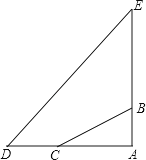

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知凸四边形ABCD中，∠A=∠C=90°．

    （1）如图1，若DE平分∠ADC，BF平分∠ABC的邻补角，判断DE与BF位置关系并证明．

    （2）如图2，若BF、DE分别平分∠ABC、∠ADC的邻补角，判断DE与BF位置关系并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】两个小组同时从甲地出发，匀速步行到乙地，甲乙两地相距7500米，第一组的步行速度是第二组的1.2倍，并且比第二组早15分钟到达乙地．设第二组的步行速度为x千米/小时，根据题意可列方程是（　　）
    A.﹣ =15
    B.﹣ =
    C.﹣ =15
    D.﹣ =

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知|a+b|+|a-b|-2b=0，在数轴上给出关于a，b的四种位置关系如图所示，则可能成立的有（　　）

    A. 1种 B. 2种 C. 3种 D. 4种

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用配方法解下列方程，其中应在方程的左右两边同时加上4的是（　　）
    A. -2x=5
    B. +4x=5
    C. +2x=5
    D.2 -4x=5

    查看答案和解析>>

    同步练习册答案