
【题目】如图,在△ABC中,AB=AC=2![]() ,∠BAC=120°,点D、E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为_____.
,∠BAC=120°,点D、E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为_____.

【答案】3![]() ﹣3.
﹣3.
【解析】
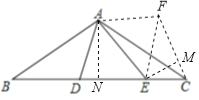
将△ABD绕点A逆时针旋转120°得到△ACF,连接EF,过点E作EM⊥CF于点M,过点A作AN⊥BC于点N,由AB=AC=2![]() 、∠BAC=120°,可得出BC=6、∠B=∠ACB=30°,通过角的计算可得出∠FAE=60°,结合旋转的性质可证出△ADE≌△AFE(SAS),进而可得出DE=FE,设CE=2x,则CM=x,EM=
、∠BAC=120°,可得出BC=6、∠B=∠ACB=30°,通过角的计算可得出∠FAE=60°,结合旋转的性质可证出△ADE≌△AFE(SAS),进而可得出DE=FE,设CE=2x,则CM=x,EM=![]() x、FM=4x-x=3x、EF=ED=6-6x,在Rt△EFM中利用勾股定理可得出关于x的一元二次方程,解之可得出x的值,再将其代入DE=6-6x中即可求出DE的长.
x、FM=4x-x=3x、EF=ED=6-6x,在Rt△EFM中利用勾股定理可得出关于x的一元二次方程,解之可得出x的值,再将其代入DE=6-6x中即可求出DE的长.
将△ABD绕点A逆时针旋转120°得到△ACF,连接EF,过点E作EM⊥CF于点M,过点A作AN⊥BC于点N,如图所示,
 ,
,
∵AB=AC=2![]() ,∠BAC=120°,
,∠BAC=120°,
∴BN=CN,∠B=∠ACB=30°,
在Rt△BAN中,∠B=30°,AB=2![]() ,
,
∴AN=![]() AB=
AB=![]() ,BN=
,BN=![]() =3,
=3,
∴BC=6,
∵∠BAC=12°,∠DAE=60°,
∴∠BAD+∠CAE=60°,
∴∠FAE=∠FAC+∠CAE=∠BAD+∠CAE=60°,
在△ADE和△AFE中, ,
,
∴△ADE≌△AFE(SAS),
∴DE=FE,
∵BD=2CE,BD=CF,∠ACF=∠B=30°,
∴设CE=2x,则CM=x,EM=![]() x,FM=4xx=3x,EF=ED=66x.
x,FM=4xx=3x,EF=ED=66x.
在Rt△EFM中,FE=66x,FM=3x,EM=![]() x,
x,
∴EF2=FM2+EM2,,即(66x)2=(3x)2+(![]() x)2,
x)2,
解得:x1=![]() ,x2=
,x2=![]() (不合题意,舍去),
(不合题意,舍去),
∴DE=66x=![]() .
.
故答案为:![]() .
.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:
【题目】在一次综合实践活动中,小明要测某地一座古塔AE的高度.如图,已知塔基顶端B(和A、E共线)与地面C处固定的绳索的长BC为80m.她先测得∠BCA=35°,然后从C点沿AC方向走30m到达D点,又测得塔顶E的仰角为50°,求塔高AE.(人的高度忽略不计,结果用含非特殊角的三角函数表示)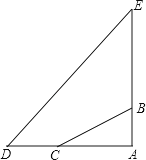
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个小组同时从甲地出发,匀速步行到乙地,甲乙两地相距7500米,第一组的步行速度是第二组的1.2倍,并且比第二组早15分钟到达乙地.设第二组的步行速度为x千米/小时,根据题意可列方程是( )
A.![]() ﹣
﹣ ![]() =15
=15
B.![]() ﹣
﹣ ![]() =
= ![]()
C.![]() ﹣
﹣ ![]() =15
=15
D.![]() ﹣
﹣ ![]() =
= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知|a+b|+|a-b|-2b=0,在数轴上给出关于a,b的四种位置关系如图所示,则可能成立的有( )
![]()
A. 1种 B. 2种 C. 3种 D. 4种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知正方形的边长为4,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的3倍,则它们第2018次相遇在边 ( )上.
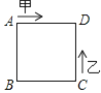
A. AB B. BC C. CD D. DA
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com