
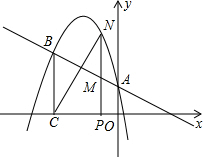
分析 (1)根据已知点的坐标利用待定系数法即可得出结论;
(2)设点N的坐标为(m,-$\frac{5}{4}$m2-$\frac{17}{4}$m+1)(-3<m<0),则点M的坐标为(m,-$\frac{1}{2}$m+1),用含m的代数式表示出来MN,结合二次函数的性质即可解决最值问题;
(3)假设存在,设点N的坐标为(m,-$\frac{5}{4}$x2-$\frac{17}{4}$x+1)(-3<m<0),连接BN、CM,当四边形BCMN为菱形时,BM与NC相互垂直平分,根据BC=MN算出m的值,从而得出点N的坐标,再去验证BN是否等于BC,由此即可得出结论.
解答 解:(1)设直线AB的解析式为:y=kx+b,
∴$\left\{\begin{array}{l}{b=1}\\{-3k+b=\frac{5}{2}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=1}\end{array}\right.$,
∴直线AB的解析式为:y=-$\frac{1}{2}$x+1;
把A(0,1),B(-3,$\frac{5}{2}$)代入y=ax2-$\frac{17}{4}$x+c得,$\left\{\begin{array}{l}{a=-\frac{5}{4}}\\{c=1}\end{array}\right.$,
∴二次函数的解析式为:y=-$\frac{5}{4}$x2-$\frac{17}{4}$x+1;
(2)设点N的坐标为(m,-$\frac{5}{4}$m2-$\frac{17}{4}$m+1)(-3<m<0),则点M的坐标为(m,-$\frac{1}{2}$m+1),
∴MN=-$\frac{5}{4}$m2-$\frac{17}{4}$m+1-(-$\frac{1}{2}$m+1)=-$\frac{5}{4}$m2-$\frac{17}{4}$m+1=-$\frac{5}{4}$(m+$\frac{3}{2}$)2+$\frac{45}{16}$,
∴当m=-$\frac{3}{2}$时,MN取最大值,最大值为$\frac{45}{16}$;
(3)假设存在,设点N的坐标为(m,-$\frac{5}{4}$m2-$\frac{17}{4}$m+1)(-3<m<0),连接BN、CM,如图所示.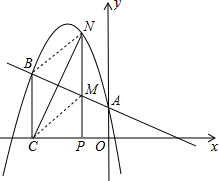
若要BM与NC相互垂直平分,只需四边形BCMN为菱形即可.
∵点B坐标为(-3,$\frac{5}{2}$),点C的坐标为(-3,0),
∴BC=$\frac{5}{2}$.
∵四边形BCMN为菱形,
∴MN=-$\frac{5}{4}$m2-$\frac{15}{4}$m=BC=$\frac{5}{2}$,
解得:m1=-2,m2=-1.
当m=-2时,点N的坐标为(-2,$\frac{9}{2}$),
∴BN=$\sqrt{(-2+3)^{2}+(\frac{9}{2}-\frac{5}{2})^{2}}$=$\sqrt{5}$,BC=$\frac{5}{2}$,BN≠BC,
故m=-2(舍去);
当m=-1时,点N的坐标为(-1,4),
∴BN=$\sqrt{(-1+3)^{2}+(4-\frac{5}{2})^{2}}$=$\frac{5}{2}$,BC=$\frac{5}{2}$,BN=BC,
∴点N(-1,4)符合题意.
故存在点N,使得BM与NC相互垂直平分,点N的坐标为(-1,4).
点评 本题考查了待定系数法求函数解析式、二次函数的性质以及菱形的性质,解题的关键是;(2)利用二次函数的性质解决最值问题;(3)根据菱形的性质确定点N的坐标.本题属于中档题,(1)(2)难度不大;(3)当确定下来四边形BCMN的形状后,问题就得以解决,解决该类型题目时,首先要想到的是将BM与NC当成对角线,根据对角线互相垂直平分能判断出四边形是什么形状,再根据该形状图形的其他性质去解决问题.


科目:初中数学 来源: 题型:填空题
 某商店经销一种品牌的洗衣机,其中某一型号的洗衣机每台进价为a元,商店将进价提高20%后作为零售价进行销售,一段时间后,商店又以9折优惠价促销,这时该型号洗衣机的零售价为1.08a元.
某商店经销一种品牌的洗衣机,其中某一型号的洗衣机每台进价为a元,商店将进价提高20%后作为零售价进行销售,一段时间后,商店又以9折优惠价促销,这时该型号洗衣机的零售价为1.08a元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
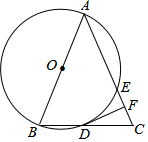 如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
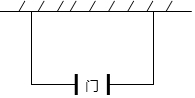 如图,某农场拟建一间饲养室,一面靠现有墙(墙足够长),且与现有墙相对的一侧墙体留有1m宽的门.已知计划中的材料可建墙体(不包括门)总长为11m,则能建成的饲养室总占地面积最大为( )m2.
如图,某农场拟建一间饲养室,一面靠现有墙(墙足够长),且与现有墙相对的一侧墙体留有1m宽的门.已知计划中的材料可建墙体(不包括门)总长为11m,则能建成的饲养室总占地面积最大为( )m2.| A. | 15 | B. | 16 | C. | 18 | D. | 24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
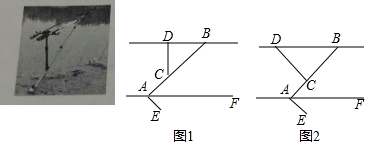
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
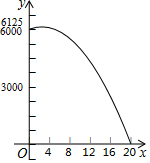 某商品的进价为每件40元,当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查,每降价1元,每星期可多卖出20件,在确保盈利的前提下,解答下列问题:
某商品的进价为每件40元,当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查,每降价1元,每星期可多卖出20件,在确保盈利的前提下,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
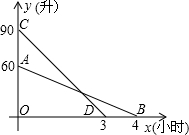 “滴滴出行”是一款涵盖出租车、专车、快车、顺风车等多项业务在内的一站式出行平台,如今已成为人们出行常用的“打车神器”,如图,分别是“滴滴出行”旗下甲、乙两辆轿车某天油箱中的剩余油量y(升)与行驶时间x(小时)的函数图象.
“滴滴出行”是一款涵盖出租车、专车、快车、顺风车等多项业务在内的一站式出行平台,如今已成为人们出行常用的“打车神器”,如图,分别是“滴滴出行”旗下甲、乙两辆轿车某天油箱中的剩余油量y(升)与行驶时间x(小时)的函数图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com