
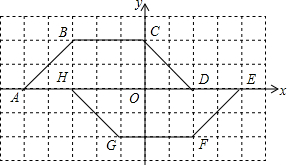
 如图,网格平面直角坐标系中,组成网格的每个小正方形的边长为单位1.
如图,网格平面直角坐标系中,组成网格的每个小正方形的边长为单位1.分析 (1)根据各点在坐标系中的位置直接写出点的坐标即可.
(2)观察图形,即可推出答案;
(3)分5种情况分别讨论即可求得;
(4)经过多边形对称中心的直线平分此多边形,求得即可.
解答 解:(1)A(-5,0)、B(-3,2)、C(0,2)、D(2,0)、E(4,0)、F(2,-2)、G(-1,-2)、H(-3,0);
(2)多边形ABCDEFGH是中心对称图形,对称中心的坐标为(-$\frac{1}{2}$,0);
(3)当0≤t≤2时,s=2t,
当2<t≤3时,s=2t+$\frac{1}{2}$(t-2)•$\frac{1}{2}$(t-2)=1+t+$\frac{1}{4}$t2;
当3<t≤6时,s=$\frac{1}{2}$(3+7)×2-$\frac{1}{2}$(7-t)•$\frac{1}{2}$(7-t)+$\frac{1}{2}$(t-2)•$\frac{1}{2}$(t-2)=$\frac{5}{2}$t+$\frac{25}{4}$;
当6<t≤7时,s=$\frac{1}{2}$(3+7)-$\frac{1}{2}$(7-t)•$\frac{1}{2}$(7-t)+$\frac{1}{2}$(t-2+t-6)×2=-$\frac{1}{4}$t2+$\frac{11}{2}$t-$\frac{41}{4}$;
当7<t≤9时,s=$\frac{1}{2}$(3+7)×2+$\frac{1}{2}$(t-2+t-6)×2=2t+2.
综上,s与t的函数关系式为:s=$\left\{\begin{array}{l}{2t(0≤t≤2)}\\{\frac{1}{4}{t}^{2}+t+1(2<t≤3)}\\{\frac{5}{2}t+\frac{25}{4}(3<t≤6)}\\{-\frac{1}{4}{t}^{2}+\frac{11}{2}t-\frac{41}{4}(6<t≤7)}\\{2t+2(7<t≤9)}\end{array}\right.$;
(4)因为多边形ABCDEFGH是中心对称图形,所以经过对称中心的直线平分此多边形;
∴平行于AB的直线移动到点(-$\frac{1}{2}$,0)时,直线平分此多边形的面积,
∴此时,t=4.5,
∴当t=4.5时,运动的直线平分此多边形的面积.
点评 本题是几何变换的综合题,考查了三角形的面积,梯形的面积,等腰直角三角形的面积,中心对称的定义和性质,分类讨论思想的运用是解题的关键.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
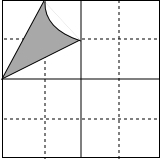 如图,已知网格中每个小正方形的边长为都是1,图中的阴影部分图案是一条以格点为圆心,以1为半径的圆弧和两条线段围成.
如图,已知网格中每个小正方形的边长为都是1,图中的阴影部分图案是一条以格点为圆心,以1为半径的圆弧和两条线段围成.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 28.3×108 | B. | 2.83×109 | C. | 2.83×10 | D. | 2.83×107 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com