
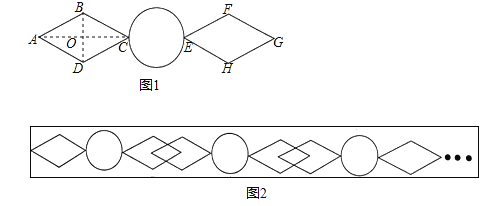
°æƒø°ø∫œ∑ –¥Ú‘Ï ¿ΩÁº∂π˙º“¬√”Œ÷––ƒ£¨æ´–ƒ…˺∆12∏ˆ«ßƒÍπ≈’Ú°£»ÁÕº1 «ƒ≥√˜«Â–°‘∫Œß«Ω÷–µƒæ´√¿Õº∞∏£¨À¸ «¡Ω∏ˆ–Œ◊¥¥Û–°œýÕ¨µƒ¡‚–Œ”Γª∏ˆ‘≤◊È≥…£¨«“A°¢C°¢E°¢G‘⁄∆‰∂‘≥∆÷·AG…œ.“—÷™¡‚–Œµƒ±þ≥§∫Õ‘≤µƒ÷±æ∂∂º «1dm£¨°œA= 60°„.

£®1£©«ÛÕº∞∏÷–AGµƒ≥§£ª
£®2£©ºŸ…Ë–°‘∫µƒŒß«Ω“ª≤ý”√…œ ˆÕº∞∏»ÁÕº2≈≈¡–£¨∆‰÷–µ⁄∂˛øÈÕº∞∏◊Û±þ¡‚–Œ“ª∏ˆ∂•µ„’˝∫√æ≠π˝µ⁄“ªøÈÕº∞∏µƒ”“±þ¡‚–Œµƒ∂‘≥∆÷––ƒ£¨....,“‘¥À¿ýÕ∆£¨µ⁄101øÈ’‚÷÷Õº∞∏’‚—˘≈≈¡–≥§Œ™∂ý…Ÿm£ø£®≤ªøº¬«∑Ïœ∂º∞∆¥Ω”¥¶£©

°æ¥∞∏°ø£®1£©AG=(![]() )dm£ª£®2£©
)dm£ª£®2£©![]() m
m
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©¡¨Ω”BD£¨ACΩª”⁄O£¨”…”⁄Àƒ±þ–ŒABCD «¡‚–Œ£¨µ√µΩAC°ÕBD£¨Ω‚÷±Ω«»˝Ω«–Œµ√µΩAO=![]() £¨”⁄ «µ√µΩΩ·¬€£ª
£¨”⁄ «µ√µΩΩ·¬€£ª
£®2£©∏˘æð“‚µ√£¨AG=![]() £¨”⁄ «µ√µΩŒß«Ω“ª≤ý≈≈¡–nøȵƒ◊Ð≥§
£¨”⁄ «µ√µΩŒß«Ω“ª≤ý≈≈¡–nøȵƒ◊Ð≥§![]() +£®n©Å1£©£®
+£®n©Å1£©£®![]() +1£©£¨º¥ø…µ√µΩΩ·¬€£Æ
+1£©£¨º¥ø…µ√µΩΩ·¬€£Æ
‘Ã‚Ω‚Œˆ£∫Ω‚£∫£®1£©¡¨Ω”BD£¨ACΩª”⁄O£Æ°þÀƒ±þ–ŒABCD «¡‚–Œ£¨°ýAC°ÕBD£Æ°þAB=1£¨°œA=60°„£¨°ý°œBAO=30°„£¨°ýAO=![]() £¨°ýAC=
£¨°ýAC=![]() £Æ°þ‘≤µƒ÷±æ∂∂º «1dm£¨°ýAG=£®
£Æ°þ‘≤µƒ÷±æ∂∂º «1dm£¨°ýAG=£®![]() £©dm£ª
£©dm£ª
£®2£©∏˘æð“‚µ√£∫AG=![]() £¨∂¯Œß«Ω“ª≤ý≈≈¡–nøȵƒ◊Ð≥§£∫
£¨∂¯Œß«Ω“ª≤ý≈≈¡–nøȵƒ◊Ð≥§£∫ ![]() +£®n©Å1£©£®
+£®n©Å1£©£®![]() +1£©£¨°ýµ⁄101øÈ’‚÷÷Õº∞∏’‚—˘≈≈¡–≥§Œ™
+1£©£¨°ýµ⁄101øÈ’‚÷÷Õº∞∏’‚—˘≈≈¡–≥§Œ™![]() +£®101©Å1£©£®
+£®101©Å1£©£®![]() +1£©=£®
+1£©=£®![]() £©dm=
£©dm=![]() √◊£Æ
√◊£Æ


 º‚◊”…˙–¬øŒÃ√øŒ ±◊˜“µœµ¡–¥∞∏
º‚◊”…˙–¬øŒÃ√øŒ ±◊˜“µœµ¡–¥∞∏ ”¢≤≈º∆ªÆÕ¨≤ΩøŒ ±∏þ–ß—µ¡∑œµ¡–¥∞∏
”¢≤≈º∆ªÆÕ¨≤ΩøŒ ±∏þ–ß—µ¡∑œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨°˜AOB «÷±Ω«»˝Ω«–Œ£¨°œAOB=90°„£¨±þAB”Îy÷·Ωª”⁄µ„C.

£®1£©»Ù°œA=°œAOC£¨ ‘Àµ√˜£∫°œB=°œBOC£ª
£®2£©—”≥§ABΩªx÷·”⁄µ„E£¨π˝O◊˜OD°ÕAB£¨»Ù°œDOB=°œEOB£¨°œA=°œE£¨«Û°œAµƒ∂» ˝£ª
£®3£©»ÁÕº£¨OF∆Ω∑÷°œAOM£¨°œBCOµƒ∆Ω∑÷œþΩªFOµƒ—”≥§œþ”⁄µ„P£¨°œA=40°„£¨µ±°˜ABO»∆Oµ„–˝◊™ ±£®±þAB”Îy÷·’˝∞Î÷· º÷’œýΩª”⁄µ„C£©£¨Œ °œPµƒ∂» ˝ «∑Ò∑¢…˙∏ƒ±‰£ø»Ù≤ª±‰£¨«Û∆‰∂» ˝£ª»Ù∏ƒ±‰£¨«ÎÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®1£©£®—ßœ∞–ƒµ√£©
–°∏’Õ¨—ß‘⁄—ßœ∞ÕÍ°∞‘≤°±’‚“ª’¬ƒ⁄»ð∫Û£¨∏–æıµΩ“ª–©º∏∫ŒŒ £¨»Áπ˚Ã̺”∏®÷˙‘≤£¨‘À”√‘≤µƒ÷™ ∂Ω‚æˆ£¨ø…“‘ πŒ ±‰µ√∑«≥£»ð“◊£Æ
¿˝»Á£∫»ÁÕº![]() £¨‘⁄
£¨‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() «
«![]() Õ‚“ªµ„£¨«“
Õ‚“ªµ„£¨«“![]() £¨«Û
£¨«Û![]() µƒ∂» ˝£¨»Ù“‘µ„
µƒ∂» ˝£¨»Ù“‘µ„![]() Œ™‘≤–ƒ£¨
Œ™‘≤–ƒ£¨![]() Œ™∞Îæ∂◊˜∏®÷˙‘≤°—
Œ™∞Îæ∂◊˜∏®÷˙‘≤°—![]() £¨‘Úµ„
£¨‘Úµ„![]() °¢
°¢![]() ±ÿ‘⁄°—
±ÿ‘⁄°—![]() …œ£¨
…œ£¨![]() «°—
«°—![]() µƒ‘≤–ƒΩ«£¨∂¯
µƒ‘≤–ƒΩ«£¨∂¯![]() «‘≤÷ÐΩ«£¨¥”∂¯ø…»ð“◊µ√µΩ
«‘≤÷ÐΩ«£¨¥”∂¯ø…»ð“◊µ√µΩ![]() __________
__________![]() £Æ
£Æ
£®2£©£®Œ Ã‚Ω‚æˆ£©
»ÁÕº![]() £¨‘⁄Àƒ±þ–Œ
£¨‘⁄Àƒ±þ–Œ![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨«Û
£¨«Û![]() µƒ∂» ˝£Æ
µƒ∂» ˝£Æ
–°∏’Õ¨—ß»œŒ™”√Ã̺”∏®÷˙‘≤µƒ∑Ω∑®£¨ø…“‘ πŒ ÂøÏÀŸΩ‚戣¨À˚ «’‚—˘Àºøºµƒ£∫![]() µƒÕ‚Ω”‘≤æÕ «“‘
µƒÕ‚Ω”‘≤æÕ «“‘![]() µƒ÷–µ„Œ™‘≤–ƒ£¨
µƒ÷–µ„Œ™‘≤–ƒ£¨![]() ≥§Œ™∞Îæ∂µƒ‘≤£ª
≥§Œ™∞Îæ∂µƒ‘≤£ª![]() µƒÕ‚Ω”‘≤“≤ «“‘
µƒÕ‚Ω”‘≤“≤ «“‘![]() µƒ÷–µ„Œ™‘≤–ƒ£¨
µƒ÷–µ„Œ™‘≤–ƒ£¨![]() ≥§Œ™∞Îæ∂µƒ‘≤£Æ’‚—˘
≥§Œ™∞Îæ∂µƒ‘≤£Æ’‚—˘![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() Àƒµ„‘⁄Õ¨“ª∏ˆ‘≤…œ£¨Ω¯∂¯ø…“‘¿˚”√‘≤÷ÐΩ«µƒ–‘÷ «Û≥ˆ
Àƒµ„‘⁄Õ¨“ª∏ˆ‘≤…œ£¨Ω¯∂¯ø…“‘¿˚”√‘≤÷ÐΩ«µƒ–‘÷ «Û≥ˆ![]() µƒ∂» ˝£¨«Î‘À”√–°∏’µƒÀº¬∑Ω‚æˆ’‚∏ˆŒ £Æ
µƒ∂» ˝£¨«Î‘À”√–°∏’µƒÀº¬∑Ω‚æˆ’‚∏ˆŒ £Æ
£®3£©£®Œ ÂÕÿ’π£©
»ÁÕº![]() £¨‘⁄
£¨‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() «
«![]() ±þ…œµƒ∏þ£¨«“
±þ…œµƒ∏þ£¨«“![]() £¨
£¨![]() £¨«Û
£¨«Û![]() µƒ≥§£Æ
µƒ≥§£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“ªÃıπ´¬∑–ÞµΩ∫˛±þ ±£¨–Ëπ’Õ‰»∆∫˛∂¯π˝£¨»Áπ˚µ⁄“ª¥Œπ’µƒΩ«°œA «120°„£¨µ⁄∂˛¥Œπ’µƒΩ«°œB «150°„£¨µ⁄»˝¥Œπ’µƒΩ« «°œC£¨’‚ ±µƒµ¿¬∑«°∫√∫Õµ⁄“ª¥Œπ’Õ‰÷Æ«∞µƒµ¿¬∑∆Ω––£¨‘Ú°œCµƒ¥Û–° «( )

A. 150°„ B. 130°„ C. 140°„ D. 120°„
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨”–“ª∏ˆµ»—¸÷±Ω«»˝Ω«–ŒAOB£¨°œOAB£Ω90°„£¨÷±Ω«±þAO‘⁄x÷·…œ£¨«“AO£Ω1£ÆΩ´Rt°˜AOB»∆‘≠µ„OÀ≥ ±’Ζ˝◊™90°„µ√µΩµ»—¸÷±Ω«»˝Ω«–ŒA1OB1£¨«“A1O£Ω2AO£¨‘ŸΩ´Rt°˜A1OB1»∆‘≠µ„OÀ≥ ±’Ζ˝◊™90°„µ√µΩµ»—¸»˝Ω«–ŒA2OB2£¨«“A2O£Ω2A1O°≠°≠“¿¥Àπʬ…£¨µ√µΩµ»—¸÷±Ω«»˝Ω«–ŒA2 017OB2 017£Æ‘Úµ„B2 017µƒ◊¯±Í£®°°°°£©

A. £®22 017£¨£≠22 017£© B. £®22 016£¨£≠22 016£© C. £®22 017£¨22 017£© D. £®22 016£¨22 016£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨æÿ–ŒABCO÷–£¨µ„C‘⁄x÷·…œ£¨µ„A‘⁄y÷·…œ£¨µ„Bµƒ◊¯±Í «£®“ª6£¨8£©£Ææÿ–ŒABCO—ÿ÷±œþBD’€µ˛£¨ πµ√µ„A¬‰‘⁄∂‘Ω«œþOB…œµƒµ„E¥¶£¨’€∫€”ÎOA°¢x÷·∑÷±Ωª”⁄µ„D°¢F£Æ

(1)÷±Ω”–¥≥ˆœþ∂ŒBOµƒ≥§£∫
(2)«Ûµ„Dµƒ◊¯±Í£ª
(3)»Ùµ„N «∆Ω√ʃ⁄»Œ“ªµ„£¨‘⁄x÷·…œ «∑ҥʑ⁄µ„M£¨ πæ◊M°¢N°¢E°¢OŒ™∂•µ„µƒÀƒ±þ–Œ «¡‚–Œ£ø»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆ¬˙◊„Ãıº˛µƒµ„Mµƒ◊¯±Í£∫»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™µ„O£®0,0£©£¨A(2,1),≈◊ŒÔœþ![]() £∫
£∫ ![]() (hŒ™≥£ ˝)”Îy÷·µƒΩªµ„Œ™B.
(hŒ™≥£ ˝)”Îy÷·µƒΩªµ„Œ™B.
£®1£©»Ùtæ≠π˝µ„A,«ÛÀ¸µƒΩ‚Œˆ Ω£¨≤¢–¥≥ˆ¥À ±tµƒ∂‘≥∆÷·º∞∂•µ„◊¯±Í£ª
£®2£©…˵„Bµƒ◊ð◊¯±Í![]() £¨«Û
£¨«Û![]() µƒ◊Ó¥Û÷µ£¨¥À ±
µƒ◊Ó¥Û÷µ£¨¥À ±![]() …œ”–¡Ωµ„£®
…œ”–¡Ωµ„£®![]() £©£¨£®
£©£¨£®![]() £©£¨∆‰÷–
£©£¨∆‰÷–![]() >
>![]() £¨±»Ωœ
£¨±»Ωœ![]() ”Î
”Î![]() µƒ¥Û.
µƒ¥Û.

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∂˛¥Œ∫Ø ˝y=ax2+bx+c£®a°Ÿ0£©µƒÕºœÛ”Îx÷·Ωª”⁄µ„A£®©Å2£¨0£©°¢B£®x1£¨0£©£¨«“1£ºx1£º2£¨”Îy÷·’˝∞Î÷·µƒΩªµ„‘⁄£®0£¨2£©µƒ…œ∑Ω£¨∂•µ„Œ™C£Æ÷±œþy=kx+m£®k°Ÿ0£©æ≠π˝µ„C°¢B£Æ‘Úœ¬¡–Ω·¬€£∫¢Ÿb£æa£ª¢⁄2a©Åb£æ©Å1£ª¢€2a+c£º0£ª¢Ðk£æa+b£ª¢ðk£º©Å1. ∆‰÷–’˝»∑µƒΩ·¬€”–_________£Æ£®ÃÓ–Ú∫≈£©

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®1£©»ÁÕº1£¨‘⁄![]() ÷–£¨∑÷±“‘
÷–£¨∑÷±“‘![]() °¢
°¢![]() Œ™–±±þ£¨œÚ
Œ™–±±þ£¨œÚ![]() µƒ–ŒÕ‚◊˜µ»—¸÷±Ω«»˝Ω«–Œ£¨÷±Ω«µƒ∂•µ„∑÷±Œ™
µƒ–ŒÕ‚◊˜µ»—¸÷±Ω«»˝Ω«–Œ£¨÷±Ω«µƒ∂•µ„∑÷±Œ™![]() £¨µ„
£¨µ„![]() ∑÷±Œ™
∑÷±Œ™![]() ±þµƒ÷–µ„.Œ £∫
±þµƒ÷–µ„.Œ £∫ ![]() «∑Ò»´µ»£ø____£®ÃÓ°∞ «°±ªÚ°∞∑Ò°±£©£ª
«∑Ò»´µ»£ø____£®ÃÓ°∞ «°±ªÚ°∞∑Ò°±£©£ª
£®2£©»ÁÕº2£¨‘⁄![]() ÷–£¨∑÷±“‘
÷–£¨∑÷±“‘![]() Œ™µ◊±þ£¨œÚ
Œ™µ◊±þ£¨œÚ![]() µƒ–ŒÕ‚◊˜µ»—¸»˝Ω«–Œ£¨∂•Ω«µƒ∂•µ„∑÷±Œ™
µƒ–ŒÕ‚◊˜µ»—¸»˝Ω«–Œ£¨∂•Ω«µƒ∂•µ„∑÷±Œ™![]() £¨«“
£¨«“![]() .µ„
.µ„![]() ∑÷±Œ™
∑÷±Œ™![]()
![]() ±þµƒ÷–µ„.
±þµƒ÷–µ„.
¢Ÿ ‘≈–∂œ![]() «∑Ò¬˙◊„£®1£©÷–µƒπÿœµ£ø»Ù¬˙◊„£¨«ÎÀµ√˜¿Ì”…£ª»Ù≤ª¬˙◊„£¨«Î–¥
«∑Ò¬˙◊„£®1£©÷–µƒπÿœµ£ø»Ù¬˙◊„£¨«ÎÀµ√˜¿Ì”…£ª»Ù≤ª¬˙◊„£¨«Î–¥![]() ÷ƺ‰¥Ê‘⁄µƒ“ª÷÷πÿœµ£¨≤¢º”“‘Àµ√˜.
÷ƺ‰¥Ê‘⁄µƒ“ª÷÷πÿœµ£¨≤¢º”“‘Àµ√˜.
¢⁄»Ù![]() £¨
£¨ ![]() £¨
£¨ ![]() µƒ√ʪ˝Œ™32£¨«Û
µƒ√ʪ˝Œ™32£¨«Û![]() µƒ√ʪ˝.
µƒ√ʪ˝.

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com