
分析 (1)根据二次根式的性质,可得a=$\sqrt{{a}^{2}}$ (a≥0),根据二次根式的乘法:$\sqrt{a}$$•\sqrt{b}$=$\sqrt{a•b}$,可得答案;
(2)根据二次根式的性质,可得a=$\sqrt{{a}^{2}}$ (a≥0),根据二次根式的乘法:$\sqrt{a}$$•\sqrt{b}$=$\sqrt{a•b}$,可得答案.
解答 解:(1)2$\sqrt{\frac{2}{3}}$=$\sqrt{4}$×$\sqrt{\frac{2}{3}}$=$\sqrt{4×\frac{2}{3}}$=$\sqrt{\frac{8}{3}}$=$\sqrt{\frac{6+2}{3}}$=$\sqrt{2+\frac{2}{3}}$,
3$\sqrt{\frac{3}{8}}$=$\sqrt{9}$×$\sqrt{\frac{3}{8}}$=$\sqrt{9×\frac{3}{8}}$=$\sqrt{\frac{27}{8}}$=$\sqrt{\frac{24}{8}+\frac{3}{8}}$=$\sqrt{3+\frac{3}{8}}$,
…
(2)a$\sqrt{\frac{a}{{a}^{2}-1}}$=$\sqrt{a+\frac{a}{{a}^{2}-1}}$,理由如下:
$\sqrt{\frac{a}{{a}^{2}-1}}$=$\sqrt{{a}^{2}}$$•\sqrt{\frac{a}{{a}^{2}-1}}$=$\sqrt{{a}^{2}•\frac{a}{{a}^{2}-1}}$=$\sqrt{\frac{{a}^{3}}{{a}^{2}-1}}$=$\sqrt{\frac{{(a}^{3}-a)+a}{{a}^{2}-1}}$=$\sqrt{\frac{a({a}^{2}-1)+a}{{a}^{2}-1}}$=$\sqrt{a+\frac{a}{{a}^{2}-1}}$.
点评 本题考查了二次根式的性质与化简,利用二次根式的乘法是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
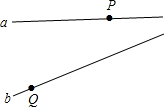 如图所示,直线a,b分别代表公路和河流,点P代表公路a上的公共汽车站,点Q
如图所示,直线a,b分别代表公路和河流,点P代表公路a上的公共汽车站,点Q查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省梅州市七年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图,将一块直角三角板的直角顶点放在直尺的一边上.如果∠1=50°,那么∠2的度数是( )

A. 30° B. 40° C. 50° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省梅州市七年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图,直线AB∥CD,CA平分∠BCD,若∠1=50°,则∠2=( ).
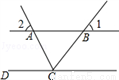
A. 65° B. 50° C. 40° D. 30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com