
分析 (1)根据①可知b=0或c=0(a≠0),那么本题可分两种情况进行讨论:
①当b=0,可联立②③,求出a,c的值,然后根据a<b<c判断出符合条件的a,c的值,进而可求出抛物线的解析式;
②当c=0时,方法同一.综合两种情况可得出抛物线的解析式;
(2)要分两种情况进行讨论:当P点在第一象限时,S△APC=S△AOC实际就是S△DPC=S△AOD.
△AOD中,根据OA,OD的长,可求出△AOD的面积.
△DPC中,可以CD为底边,P点的纵坐标为高,
过P作PG⊥x轴于G,OG就是△DPC的高.
可根据相似三角形ADO和APG,得出关于OD,PG,OA,OG的比例关系式.
设出P点的坐标,即可根据所得的比例关系式求出P点的坐标.
②在第二象限内,可分别过C,A作坐标轴的平行线,可得出一个矩形,设两条平行线的交点为Q,那么△AQC与△AOC的面积相等,而P在△ACQ内,因此△ACP的面积总小于△ACQ的面积.因此△ACP的面积不会和△ACO的面积相等.此种情况不成立.
解答 解:(1)∵a≠0,abc=0,
∴bc=0
①当b=0时:
由$\left\{\begin{array}{l}{a+b+c=3}\\{ab+ac+bc=-4}\end{array}\right.$,
得$\left\{\begin{array}{l}{a+c=3}\\{ac=-4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{a}_{1}=-1}\\{{c}_{1}=4}\end{array}\right.$.
或$\left\{\begin{array}{l}{{a}_{2}=4}\\{{c}_{2}=-1}\end{array}\right.$,
∵a<b<c.
∴$\left\{\begin{array}{l}{{a}_{2}=4}\\{{c}_{2}=-1}\end{array}\right.$(不合题意,舍去),
∴a=-1,b=0,c=4
②当c=0时,
由$\left\{\begin{array}{l}{a+b+c=3}\\{ab+ac+bc=-4}\end{array}\right.$,
得$\left\{\begin{array}{l}{a+b=3}\\{ab=-4}\end{array}\right.$,
解之得$\left\{\begin{array}{l}{{a}_{1}=4}\\{{b}_{1}=-1}\end{array}\right.$或$\left\{\begin{array}{l}{{a}_{2}=-1}\\{{b}_{2}=4}\end{array}\right.$,
∵a<b<c;
∴$\left\{\begin{array}{l}{{a}_{1}=4}\\{{b}_{1}=-1}\end{array}\right.$和$\left\{\begin{array}{l}{{a}_{2}=-1}\\{{b}_{2}=4}\end{array}\right.$,都不合题意,舍去.
∴所求的抛物线解析式为y=-x2+4.
(2)分两种情况讨论:
①在第一象限内,设在抛物线上存在点P(m,n),使得S△APC=S△AOC.
过P作PM⊥x轴于点M,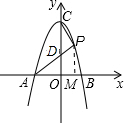
则m>0,n>0,n=-m2+4
OM=m,PM=-m2+4,OA=2,AM=m+2
设APn交y轴于点Dn,设OD=t
∵OD∥PM,
∴$\frac{OA}{AM}$=$\frac{OD}{PM}$即$\frac{2}{m+2}$=$\frac{t}{-{m}^{2}+4}$,
整理得:mt+2t=8-2m2,DC=OC-OD=4-t
S△AOD=$\frac{1}{2}$OA•OD=$\frac{1}{2}$×2×t=t;
S△PCD=$\frac{1}{2}$CD•OM=$\frac{1}{2}$(4-t)×m;
∵S△AOC=S△APC
∴S△AOD=S△PCD
即t=$\frac{1}{2}$(4-t)×m,mt+2t=4m
将mt+2t=4m代入mt+2t=8-2m2中有8-2m2=4m
整理得m2+2m-4=0,m1=$\sqrt{5}$-1,m2=-1-$\sqrt{5}$
∵m>0,
∴m2=-1-$\sqrt{5}$(不合题意,舍去)
∴m=$\sqrt{5}$-1,
此时n=-m2+4=-($\sqrt{5}$-1)2+4=2$\sqrt{5}$-2
∴存在点P坐标为($\sqrt{5}$-1,2$\sqrt{5}$-2);
②使得S△APC=S△AOC在第二象限内,这条抛物线上任取一点P′,连接P′A,P′C,分别过点A作直线l1垂直x轴,过点C作直线l2垂直于y轴,l1与l2相交于Q点,则四边形QAOC是矩形,S△AQC=S△AOC.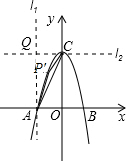
设P′点坐标为(m′,n′)
则有-2<m′<0
∵n′=-m′2+4
∴0<n′<4
∴点P′在矩形QAOC内,又易知P′在△AQC内
∴S△AP′C<S△AQC,S△AP′C<S△AOC
∴在第二象限内这条抛物线上不存在点Pnn,使S△APC=S△AOC.
点评 本题结合三角形的相关知识考查了二次函数的综合应用,由于题中的数据较多,计算过程较复杂,因此细心求解是解题的关键.


科目:初中数学 来源: 题型:填空题
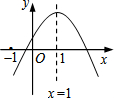 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0; ②a-b+c<0; ③当x<0时,y<0;④方程ax2+bx+c=0(a≠0)有两个大于-1的实数根. 其中错误的结论有①③.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0; ②a-b+c<0; ③当x<0时,y<0;④方程ax2+bx+c=0(a≠0)有两个大于-1的实数根. 其中错误的结论有①③.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
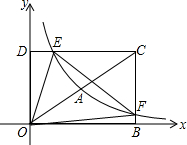 如图,在平面直角坐标系中,矩形DOBC的顶点O与坐标原点重合,B、D分别在坐标轴上,点C的坐标为(6,4),反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.
如图,在平面直角坐标系中,矩形DOBC的顶点O与坐标原点重合,B、D分别在坐标轴上,点C的坐标为(6,4),反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
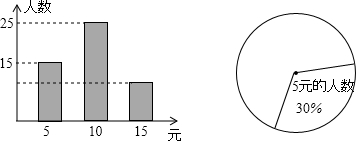
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com