
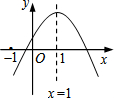 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0; ②a-b+c<0; ③当x<0时,y<0;④方程ax2+bx+c=0(a≠0)有两个大于-1的实数根. 其中错误的结论有①③.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0; ②a-b+c<0; ③当x<0时,y<0;④方程ax2+bx+c=0(a≠0)有两个大于-1的实数根. 其中错误的结论有①③. 分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点得出c的值,然后根据抛物线与x轴交点的个数及x=-1时二次函数的值的情况进行推理,进而对所得结论进行判断.
解答 解:①由二次函数的图象开口向下可得a<0,由抛物线与y轴交于x轴上方可得c>0,则ac<0.故①错误;
②根据图示知,当x=-1时,y<0,即a-b+c<0.故②正确;
③根据图示知,当x<-1时,y<0.故③错误;
④由图示知,抛物线与x轴有两个不相同的交点,且这两个交点都在x=-1的右边,所以方程ax2+bx+c=0(a≠0)有两个大于-1的实数根.故④正确;
综上所述,错误的结论有:①③.
故答案是:①③.
点评 此题主要考查了图象与二次函数系数之间的关系,二次函数与方程之间的转换,会利用特殊值代入法求得特殊的式子,如:y=a-b+c,然后根据图象判断其值.


科目:初中数学 来源: 题型:选择题
 如图,小明课间把老师的三角板的直角顶点放在两条平行线a、b上,已知∠1=55°,则∠2的度数为( )
如图,小明课间把老师的三角板的直角顶点放在两条平行线a、b上,已知∠1=55°,则∠2的度数为( )| A. | 35° | B. | 45° | C. | 55° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为方便住校生晚自习后回到宿舍就寝,赵化中学新安装了一批照明路灯;一天上午小刚在观看新安的照明灯时,发现在太阳光的正面照射下,照明灯的灯杆的投影的末端恰好落在2.5米高文化走廊墙的顶端,小刚测得照明灯的灯杆的在太阳光下的投影从灯杆的杆脚到文化走廊的墙脚的影长为4.6米,同一时刻另外一个前来观看照明路灯小静测得身高1.5米小刚站立时在太阳光下的影长恰好为1米,请同学们画出与问题相关联的线条示意图并求出新安装的照明路灯的灯杆的高度?
为方便住校生晚自习后回到宿舍就寝,赵化中学新安装了一批照明路灯;一天上午小刚在观看新安的照明灯时,发现在太阳光的正面照射下,照明灯的灯杆的投影的末端恰好落在2.5米高文化走廊墙的顶端,小刚测得照明灯的灯杆的在太阳光下的投影从灯杆的杆脚到文化走廊的墙脚的影长为4.6米,同一时刻另外一个前来观看照明路灯小静测得身高1.5米小刚站立时在太阳光下的影长恰好为1米,请同学们画出与问题相关联的线条示意图并求出新安装的照明路灯的灯杆的高度?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC,AE延长线的交点,AG与CD相交于点F.
如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC,AE延长线的交点,AG与CD相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com