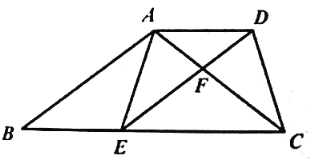
【题目】如图，已知梯形
中，
,
，
是边
上的点，且
，
交
于点
.
求证：
；
当
时，求证：
.
【答案】（1）详见解析；（2）详见解析
【解析】
（1）由一线三等角，可得
,故
．
（2）只要证明四边形ADEB是平行四边形即可解决问题．
（1）∵AD∥BC，
∴∠DAC=∠ACB，
∵AB=AC，
∴∠B=∠ACB，
∴∠DAF=∠B，
∵∠AEC=∠AED+∠DEC=∠B+∠BAE，∠AED=∠CAD=∠ACB，
∴∠DEC=∠BAE，
∵AD∥BC，
∴∠DEC=∠ADF，
∴∠BAE=∠ADF，
∴△ABE∽△DAF；
（2）∵ACFC=AEEC，AC=AB，
∴ABFC=AEEC，
∴
，
∵∠B=∠FCE，∠BAE=∠FEC，
∴△BAE∽△CEF，
∴
，
∴
，
∴FC=EF，
∴∠FEC=∠FCE，
∵∠FCE=∠B，
∴∠B=∠FEC，
∴AB∥DE，
∵AD∥BE，
∴四边形ADEB是平行四边形，
∴AD=BE．
应用题天天练四川大学出版社系列答案科目：初中数学 来源： 题型：
【题目】如图，抛物线y＝ax2+bx+3(a≠0)的对称轴为直线x＝﹣1，抛物线交x轴于A、C两点，与直线y＝x﹣1交于A、B两点，直线AB与抛物线的对称轴交于点E．
(1)求抛物线的解板式．
(2)点P在直线AB上方的抛物线上运动，若△ABP的面积最大，求此时点P的坐标．
(3)在平面直角坐标系中，以点B、E、C、D为顶点的四边形是平行四边形，请直接写出符合条件点D的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（题文）如图，在矩形ABCD中，点E是AD上的一个动点，连接BE，作点A关于BE的对称点F，且点F落在矩形ABCD的内部，连结AF，BF，EF，过点F作GF⊥AF交AD于点G，设 
=n.
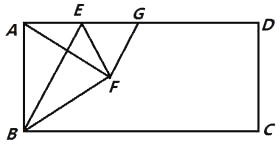
（1）求证：AE=GE；
（2）当点F落在AC上时，用含n的代数式表示
的值；
（3）若AD=4AB，且以点F，C，G为顶点的三角形是直角三角形，求n的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了加强学生的安全意识，某校组织了学生参加安全知识竞赛，从中抽取了部分学生成绩进行统计，并按照成绩从低到高分成A，B，C，D，E五个小组，绘制统计图如下（未完成），解答下列问题：
（1）样本容量为 ，频数分布直方图中a＝ ；
（2）扇形统计图中D小组所对应的扇形圆心角为n°，求n的值并补全频数分布直方图；
（3）若成绩在80分以上（不含80分）为优秀，全校共有2000名学生，估计成绩优秀的学生有多少名？
查看答案和解析>>
科目：初中数学 来源： 题型：
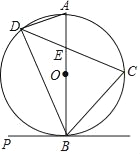
【题目】如图，C、D是以AB为直径的⊙O上的点，
，弦CD交AB于点E．
（1）当PB是⊙O的切线时，求证：∠PBD=∠DAB；
（2）求证：BC2﹣CE2=CEDE；
（3）已知OA=4，E是半径OA的中点，求线段DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个不透明的袋子中装有红、白两种颜色的小球，这些球除颜色外完全相同，其中红球有
个，若从中随机摸出一个球，这个球是白球的概率为
．
（
）请直接写出袋子中白球的个数．
（
）随机摸出一个球后，放回并搅匀，再随机摸出一个球，求两次都摸到相同颜色的小球的概率．（请结合树状图或列表解答）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，小巷左右两侧是竖直的墙，一架梯子AC斜靠在右墙，测得梯子顶端距离地面AB＝2米，梯子与地面夹角α的正弦值sinα＝0.8．梯子底端位置不动，将梯子斜靠在左墙时，顶端距离地面2.4米，则小巷的宽度为( )
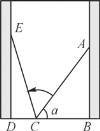
A. 0.7米B. 1.5米
C. 2.2米D. 2.4米
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店经营一种文化衫，已知成批购进时的单价是20元．调查发现：销售单价是30元时，月销售量是230件，而销售单价每上涨1元，月销售量就减少10件，但每件文化衫售价不能高于40元．设每件文化衫的销售单价上涨了
元时（为正整数），月销售利润为
元．
（1）求与的函数关系式并直接写出自变量的取值范围．
（2）每件文化衫的售价定为多少元时可使月销售利润最大？最大的月利润是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
