
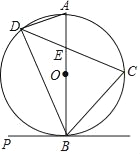
【题目】如图,C、D是以AB为直径的⊙O上的点,![]() ,弦CD交AB于点E.
,弦CD交AB于点E.
(1)当PB是⊙O的切线时,求证:∠PBD=∠DAB;
(2)求证:BC2﹣CE2=CEDE;
(3)已知OA=4,E是半径OA的中点,求线段DE的长.
【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】
(1)由AB是⊙O的直径知∠BAD+∠ABD=90°,由PB是⊙O的切线知∠PBD+∠ABD=90°,据此可得答案;
(2)连接OC,设圆的半径为r,则OA=OB=OC=r,证△ADE∽△CBE得DECE=AEBE=r2-OE2,由![]() 知∠AOC=∠BOC=90°,根据勾股定理知CE2=OE2+r2、BC2=2r2,据此得BC2-CE2=r2-OE2,从而得证;
知∠AOC=∠BOC=90°,根据勾股定理知CE2=OE2+r2、BC2=2r2,据此得BC2-CE2=r2-OE2,从而得证;
(3)先求出BC=4![]() 、CE=2
、CE=2![]() ,根据BC2-CE2=CEDE计算可得.
,根据BC2-CE2=CEDE计算可得.
(1)∵AB是⊙O的直径,
∴∠ADB=90°,即∠BAD+∠ABD=90°,
∵PB是⊙O的切线,
∴∠ABP=90°,即∠PBD+∠ABD=90°,
∴∠BAD=∠PBD;
(2)∵∠A=∠C、∠AED=∠CEB,
∴△ADE∽△CBE,
∴![]() ,即DECE=AEBE,
,即DECE=AEBE,
如图,连接OC,

设圆的半径为r,则OA=OB=OC=r,
则DECE=AEBE=(OA﹣OE)(OB+OE)=r2﹣OE2,
∵![]() ,
,
∴∠AOC=∠BOC=90°,
∴CE2=OE2+OC2=OE2+r2,BC2=BO2+CO2=2r2,
则BC2﹣CE2=2r2﹣(OE2+r2)=r2﹣OE2,
∴BC2﹣CE2=DECE;
(3)∵OA=4,
∴OB=OC=OA=4,
∴BC=![]() =4
=4![]() ,
,
又∵E是半径OA的中点,
∴AE=OE=2,
则CE=![]() =
=![]() =2
=2![]() ,
,
∵BC2﹣CE2=DECE,
∴(4![]() )2﹣(2
)2﹣(2![]() )2=DE2
)2=DE2![]() ,
,
解得:DE=![]() .
.


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次“寻宝”人找到了如图所示的两个标志点A(2,3),B(4,1),A,B两点到“宝藏”点的距离都是![]() ,则“宝藏”点的坐标是( )
,则“宝藏”点的坐标是( )
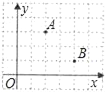
A. (1,0) B. (5,4) C. (1,0)或(5,4) D. (0,1)或(4,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A,且当钟面显示3点30分时,分针垂直于桌面,A点距桌面的高度为10公分.如图2,若此钟面显示3点45分时,A点距桌面的高度为16公分,则钟面显示3点50分时,A点距桌面的高度为多少公分()
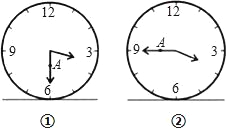
A. ![]() B. 16+π C. 18 D. 19
B. 16+π C. 18 D. 19
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个正方形AOBC各顶点的坐标分别为A(0,3),O(0,0),B(3,0),C(3,3).若以原点为位似中心,将这个正方形的边长缩小为原来的![]() ,则新正方形的中心的坐标为_____.
,则新正方形的中心的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知点A、B是反比例函数y=﹣![]() 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蓄水池的排水管每小时排水8立方米,6小时可将满池水全部排空.
(1)蓄水池的容积是多少?
(2)如果每小时排水量用Q表示,求排水时间t与Q的函数关系式.
(3)如果5小时内把满池水排完,那么每小时排水量至少是多少?
(4)已知排水管最大排水量是每小时12立方米,那么最少要多少小时才能将满池水全部排空?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝祖国70周年华诞,阳光超市销售甲、乙两种庆祝商品,该超市若同时购进甲、乙两种商品各10件共花费400元;若购进甲种商品30件,购进乙种商品15件,将用去750元;
(1)求甲、乙两种商品每件的进价;
(2)由于甲、乙两种商品受到市民欢迎,十一月份超市决定购进甲、乙两种商品共80件,且保持(1)的进价不变,已知甲种商品每件的售价为15元,乙种商品每件的售价40元,要使十一月份购进的甲、乙两种商品共80件全部销售完的总利润不少于600元,那么该超市最多购进甲种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据:![]() ≈2.449,结果保留整数)
≈2.449,结果保留整数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com