
����Ŀ��Ϊ��ף���70���껪�������ⳬ�����ۼס���������ף��Ʒ���ó�����ͬʱ�����ס���������Ʒ��10��������400Ԫ;������������Ʒ30��������������Ʒ15��������ȥ750Ԫ��
��1����ס���������Ʒÿ���Ľ��ۣ�
��2�����ڼס���������Ʒ�ܵ�����ӭ��ʮһ�·ݳ��о��������ס���������Ʒ��80�����ұ��֣�1���Ľ��۲��䣬��֪������Ʒÿ�����ۼ�Ϊ15Ԫ��������Ʒÿ�����ۼ�40Ԫ��Ҫʹʮһ�·ݹ����ļס���������Ʒ��80��ȫ�������������������600Ԫ����ô�ó�������������Ʒ���ټ���
���𰸡���1��������Ʒÿ���Ľ���Ϊ10Ԫ��������Ʒÿ���Ľ���Ϊ30Ԫ����2���ó�������������Ʒ40��
��������
��1���������Ʒÿ���Ľ���ΪxԪ��������Ʒÿ���Ľ���ΪyԪ�����ݡ��ס���������Ʒ��10��������400Ԫ��������������Ʒ30��������������Ʒ15��������ȥ750Ԫ���ж�Ԫһ�η��������ɵã�
��2���蹺��������Ʒm������������Ʒ������80-m���������ݡ�80��ȫ�������������������600Ԫ���в���ʽ���ɵã�
�⣺��1���������Ʒÿ���Ľ���ΪxԪ��������Ʒÿ���Ľ���ΪyԪ��
�������⣬�ã�![]()
��ã�![]()
�𣺼�����Ʒÿ���Ľ���Ϊ10Ԫ��������Ʒÿ���Ľ���Ϊ30Ԫ��
��2���蹺��������Ʒm������������Ʒ������80-m������
�������⣬�ã���15-10��m+��40-30����80-m����600��
��ã�m��40��
�𣺸ó�������������Ʒ40����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ϊ�˶����з���һ�ֲ�Ʒ���к������ۣ����ò�Ʒ���ⶨ�ļ۸����������ͨ����5��������������ͳ��,�õ��������ݣ�

��1��ͨ������������е����ݽ��з�������������y�������뵥��![]() ��Ԫ/����֮�����һ�κ�����ϵ����y����
��Ԫ/����֮�����һ�κ�����ϵ����y����![]() �ĺ�����ϵʽ������Ҫд�������Ա�����ȡֵ��Χ����
�ĺ�����ϵʽ������Ҫд�������Ա�����ȡֵ��Χ����
��2��Ԥ���ڽ��������У������뵥����Ȼ���ڣ�2���еĹ�ϵ���Ҹò�Ʒ�ijɱ���20Ԫ/��.Ϊʹ�������������ò�Ʒ�ĵ���Ӧ��Ϊ����?
��3��Ϊ��֤��Ʒ��ʵ�����������������õ���30�����ҹ�����õ����õ���400Ԫ����ֱ��д������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ��AD��BC��AB��BC��CD��DE��CD=ED��AD=2��BC=3������ADE�����Ϊ�� ��

A.1 B.2 C.5 D.��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������꣬���ŵ�������Ŀ��ٷ�չ�������̰�������ռ����ݼ��������ı�������������������ҵ�Ʊ���ij��վ�õ�����ͳ�Ʊ���
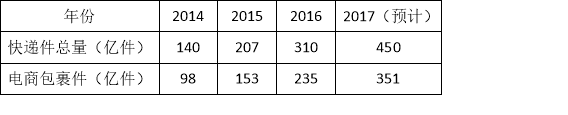
��1����ѡ���ʵ���ͳ��ͼ������2014��2017�ꡰ���̰�������ռ���ꡰ��ݼ��������İٷֱȣ���ȷ��1%����
��2����2018�ꡰ��ݼ����������ﵽ675�ڼ�����������С����̰�������ԼΪ�����ڼ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
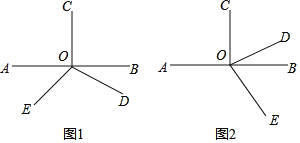
����Ŀ����֪��OΪֱ��AB�ϵ�һ�㣬��BOC����DOE��90��
��1����ͼ1��������OC������OD��ֱ��AB������ʱ����ش���۲�˵�����ɣ�
����COD�͡�BOE�����
����BOD�͡�COE��ʲô��ϵ��
��2����ͼ2��������OC������OD��ֱ��AB��ͬ��ʱ����ֱ�ӻش�
����COD�͡�BOE�����
���ڣ�1�����еġ�BOD�͡�COE�Ĺ�ϵ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() ���ʾ��
���ʾ��![]() ��
��![]() ���ʾ��6��
���ʾ��6��
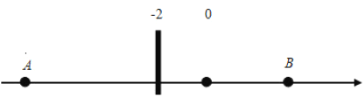
��1��A��B����֮��ľ������_________��
��2������������һ������![]() ������ʾ������
������ʾ������![]() ����
����![]() ����Сֵ��_________��
����Сֵ��_________��
��3������![]() ���
���![]() ֮��ľ����ʾΪ
֮��ľ����ʾΪ![]() ����
����![]() ���
���![]() ֮��ľ����ʾΪ
֮��ľ����ʾΪ![]() ��������������һ��
��������������һ��![]() ��ʹ
��ʹ![]() ����
����![]() ���ʾ������_________��
���ʾ������_________��
��4������ԭ��![]() �����2����λ����һ���壬һС��״ӵ�
�����2����λ����һ���壬һС��״ӵ�![]() ����5����λ/����ٶ������˶���ͬʱ��һС���Ҵӵ�
����5����λ/����ٶ������˶���ͬʱ��һС���Ҵӵ�![]() ����2����λ/����ٶ������˶������������������Ĵ�С���ɿ���һ�㣩����ֱ���ԭ�����ٶ����෴�ķ����˶������˶�ʱ��Ϊ
����2����λ/����ٶ������˶������������������Ĵ�С���ɿ���һ�㣩����ֱ���ԭ�����ٶ����෴�ķ����˶������˶�ʱ��Ϊ![]() �룬����
�룬����![]() ����ʾ�ס�����С��֮��ľ���
����ʾ�ס�����С��֮��ľ���![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ�������ABC�У�AB=2������D��B��ʼ��BC���C�˶��������C��ֹͣ�˶�������ABD�Ƶ�A��ת��õ���ACE��������˵���У���ȷ���ǣ�������
��DE����СֵΪ1����ADCE������Dz���ģ����������˶������У���E�˶���·��Ϊ2�����������˶������У���ADE���ܳ��ȱ�С����

A. �٢ۢ� B. �٢ڢ� C. �ڢۢ� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һֻС�������������ϵ�ij��![]() ����һ�δ�
����һ�δ�![]() ������һ����λ��
������һ����λ��![]() ���ڶ��δ�
���ڶ��δ�![]() ������
������![]() �����
����λ��![]() �������δ�
�������δ�![]() ������
������![]() �����
����λ��![]() �����Ĵδ�
�����Ĵδ�![]() ������
������![]() �����
����λ��![]() �������Ϲ�������
�������Ϲ�������![]() ��ʱ�������������ϵĵ�
��ʱ�������������ϵĵ�![]() ����ʾ����ǡ����2019������ֻС��ij�ʼλ��
����ʾ����ǡ����2019������ֻС��ij�ʼλ��![]() ���ڵ�����_____��
���ڵ�����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
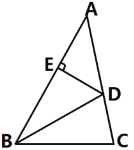
����Ŀ���ڡ�ABC�У�BDƽ�֡�ABC����AC�ڵ�D��DE��AB�ڵ�E��AB=3cm��BC=2.5cm����ABD�����Ϊ2cm2,��S��ABC=____________cm2��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com