
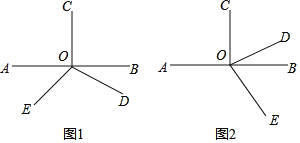
【题目】已知点O为直线AB上的一点,∠BOC=∠DOE=90°
(1)如图1,当射线OC、射线OD在直线AB的两侧时,请回答结论并说明理由;
①∠COD和∠BOE相等吗?
②∠BOD和∠COE有什么关系?
(2)如图2,当射线OC、射线OD在直线AB的同侧时,请直接回答;
①∠COD和∠BOE相等吗?
②第(1)题中的∠BOD和∠COE的关系还成立吗?
【答案】(1)①∠COD=∠BOE,理由见解析;②∠BOD+∠COE=180°,理由见解析;(2)①∠COD=∠BOE,②成立
【解析】
(1)①根据等式的性质,在直角的基础上都加∠BOD,因此相等,②将∠BOD+∠COE转化为两个直角的和,进而得出结论;
(2)①根据同角的余角相等,可得结论,②仍然可以将∠BOD+∠COE转化为两个直角的和,得出结论.
解:(1)①∠COD=∠BOE,理由如下:
∵∠BOC=∠DOE=90°,
∴∠BOC+∠BOD=∠DOE+∠BOD,
即∠COD=∠BOE,
②∠BOD+∠COE=180°,理由如下:
∵∠DOE=90°,∠AOE+∠DOE+∠BOD=∠AOB=180°,
∴∠BOD+∠AOE=180°﹣90°=90°,
∴∠BOD+∠COE=∠BOD+∠AOE+∠AOC=90°+90°=180°,
(2)①∠COD=∠BOE,
∵∠COD+∠BOD=∠BOC=90°=∠DOE=∠BOD+∠BOE,
∴∠COD=∠BOE,
②∠BOD+∠COE=180°,
∵∠DOE=90°=∠BOC,
∴∠COD+∠BOD=∠BOE+∠BOD=90°,
∴∠BOD+∠COE=∠BOD+∠COD+∠BOE+∠BOD=∠BOC+∠DOE=90°+90°=180°,
因此(1)中的∠BOD和∠COE的关系仍成立.


科目:初中数学 来源: 题型:
【题目】如图1,在正方形![]() 中,
中,![]() 是对角线,点
是对角线,点![]() 在
在![]() 上,
上,![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() ,点
,点![]() 是
是![]() 的中点,连结
的中点,连结![]() 与
与![]() .
.
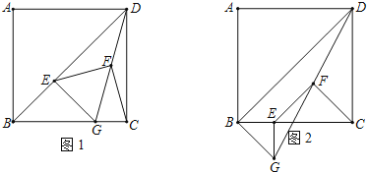
(1)求证:![]() .
.
(2)求证:![]() .
.
(3)如图2,若等腰直角三角形![]() 绕点
绕点![]() 按顺时针旋转
按顺时针旋转![]() ,其他条件不变,请判断
,其他条件不变,请判断![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题,请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长.

(1) 如图1,正方体的棱长为5cm一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处;
(2) 如图2,有一圆柱形食品盒,它的高等于16cm,底面直径为20cm.如果在盒外底面的边缘A处有一只蚂蚁,它想吃到盒外对面中点B处的食物;(盒的厚度和蚂蚁的大小忽略不计,结果可含π)
(3) 如图3, 有一无盖的圆柱形食品盒,它的高等于16cm,底面直径为20cm.如果在盒外底面的边缘A处有一只蚂蚁,它想吃到盒内对面中点B处的食物.(盒的厚度和蚂蚁的大小忽略不计,结果可含π)
查看答案和解析>>
科目:初中数学 来源: 题型:
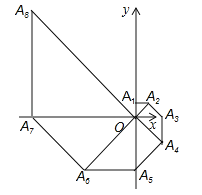
【题目】如图,在平面直角坐标系中,等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上,且OA1=A1A2=1,以OA2为直角边作第二个等腰直角三角形OA2A3,以OA3为直角边作第三个等腰直角三角形OA3A4,…,依此规律,得到等腰直角三角形OA2017A2018,则点A2017的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有四张标着数字1,2,3,4的卡片,小明、小华两人按照各自的规则玩抽卡片游戏.
小明画出树状图如图所示:
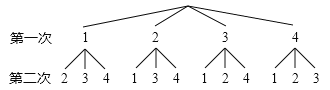
小华列出表格如下:

回答下列问题:
(1)根据小明画出的树形图分析,他的游戏规则是,随机抽出一张卡片后 (填“放回”或“不放回”),再随机抽出一张卡片;
(2)根据小华的游戏规则,表格中①表示的有序数对为 ;
(3)规定两次抽到的数字之和为奇数的获胜,你认为谁获胜的可能性大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝祖国70周年华诞,阳光超市销售甲、乙两种庆祝商品,该超市若同时购进甲、乙两种商品各10件共花费400元;若购进甲种商品30件,购进乙种商品15件,将用去750元;
(1)求甲、乙两种商品每件的进价;
(2)由于甲、乙两种商品受到市民欢迎,十一月份超市决定购进甲、乙两种商品共80件,且保持(1)的进价不变,已知甲种商品每件的售价为15元,乙种商品每件的售价40元,要使十一月份购进的甲、乙两种商品共80件全部销售完的总利润不少于600元,那么该超市最多购进甲种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=90°![]() ∠A
∠A
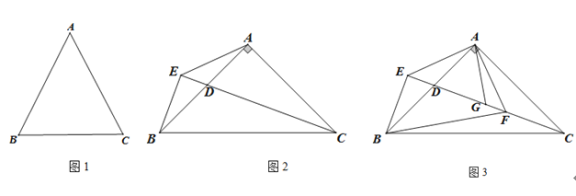
(1)如图1,求证:AB=AC;
(2)如图2,若∠BAC=90°,点D为AB上一点,过点B作直线CD的垂线,垂足为E,连接AE, 求∠AEC的度数;
(3)如图3,在(2)的条件下,过点A作AE的垂线交CE于点F,连接BF,若∠ABF-∠EAB=15°,G为DF上一点,连接AG,若∠AGD=∠EBF,AG=6,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC,现有下列结论:①DE=DF; ②DE+DF=AD; ③DM平分∠ADF; ④AB+AC=2AE,其中正确的个数有( )
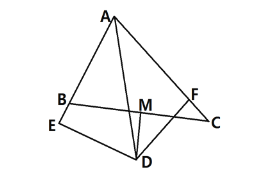
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com