
【题目】李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题,请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长.

(1) 如图1,正方体的棱长为5cm一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处;
(2) 如图2,有一圆柱形食品盒,它的高等于16cm,底面直径为20cm.如果在盒外底面的边缘A处有一只蚂蚁,它想吃到盒外对面中点B处的食物;(盒的厚度和蚂蚁的大小忽略不计,结果可含π)
(3) 如图3, 有一无盖的圆柱形食品盒,它的高等于16cm,底面直径为20cm.如果在盒外底面的边缘A处有一只蚂蚁,它想吃到盒内对面中点B处的食物.(盒的厚度和蚂蚁的大小忽略不计,结果可含π)
【答案】(1)![]() cm;(2)
cm;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)将长方体侧面展开,直接利用勾股定理得出AC1的长,进而得出答案;
(2)将圆柱侧面展开,首先求出AC的长,再利用勾股定理求出AB的长;
(3)将圆柱侧面展开,再将内部展开,首先求出AC的长,再利用勾股定理求出AB′的长.
(1)如图,将长方体侧面展开,
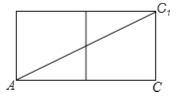
易得AC=5×2=10 cm.CC1=5cm.
在Rt△ACC1中,由勾股定理,得
![]()
答:蚂蚁需要爬行的最短路程的长为![]() cm.
cm.
(2)如图,将圆柱体侧面展开,
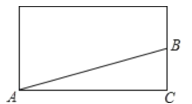
AC=2πR=2π×10÷2=10π cm,
BC=16÷2=8cm.
故![]()
=![]()
=![]()
答:蚂蚁需要爬行的最短路程的长![]() ;
;
(3)如图,将圆柱体侧面展开,再将内部展开
AC=2πR=2π×10÷2=10π cm,
BC=16÷2+16=24cm.
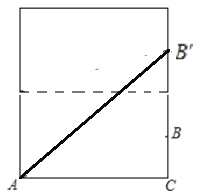
在Rt△AB′C中,由勾股定理,得
![]()
![]()
![]()
故蚂蚁需要爬行的最短路程的长![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,已知点D,E,F分别是BC,AD,CE的中点,且S△ABC=4,则S△BEF的等于( )
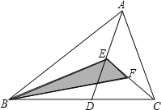
A. ![]() B. 1C. 2D. 3
B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC 中,AB=15,AC=13,高 AD=12,则△ABC 的周长是( )
A. 42B. 32C. 42 或 32D. 42 或 37
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式:
①(2a+b)(m+n);②2a(m+n)+b(m+n);③m(2a+b)+n(2a+b);④2am+2an+bm+bn,你认为其中正确的有( )

A. ①② B. ③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
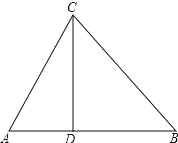
【题目】某校要在一块三角形空地上种植花草,如图所示,AC=13 米、AB=14 米、BC=15 米, 若线段 CD 是一条引水渠,且点 D 在边 AB 上.已知水渠的造价每米 150 元.问:点 D 与点 C 距离多远时,水渠的造价最低?最低造价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() (k为常数).
(k为常数).
(1)若点P1(![]() ,y1)和点P2(﹣
,y1)和点P2(﹣![]() ,y2)是该反比例函数图象上的两点,试利用反比例函数的性质比较y1和y2的大小;
,y2)是该反比例函数图象上的两点,试利用反比例函数的性质比较y1和y2的大小;
(2)设点P(m,n)(m>0)是其图象上的一点,过点P作PM⊥x轴于点M.若tan∠POM=2,PO=![]() (O为坐标原点),求k的值,并直接写出不等式kx+
(O为坐标原点),求k的值,并直接写出不等式kx+![]() >0的解集.
>0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
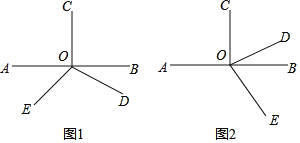
【题目】已知点O为直线AB上的一点,∠BOC=∠DOE=90°
(1)如图1,当射线OC、射线OD在直线AB的两侧时,请回答结论并说明理由;
①∠COD和∠BOE相等吗?
②∠BOD和∠COE有什么关系?
(2)如图2,当射线OC、射线OD在直线AB的同侧时,请直接回答;
①∠COD和∠BOE相等吗?
②第(1)题中的∠BOD和∠COE的关系还成立吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:

(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com