
【题目】如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC,现有下列结论:①DE=DF; ②DE+DF=AD; ③DM平分∠ADF; ④AB+AC=2AE,其中正确的个数有( )
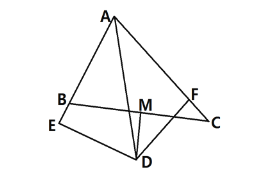
A.1个B.2个C.3个D.4个
【答案】C
【解析】
①由角平分线的性质可知①正确;②由题意可知∠EAD=∠FAD=30°,故可得ED=![]() AD,DF=
AD,DF=![]() AD,从而可证明②正确;③若DM平分∠ADF,则∠EDM=90°,从而得到∠ABC为直角三角形,条件不足,不能确定,故③错误;④证明△EBD≌△DFC和Rt△AED≌Rt△AFD,从而得到BE=FC,AE=AF,进而可证明④正确.
AD,从而可证明②正确;③若DM平分∠ADF,则∠EDM=90°,从而得到∠ABC为直角三角形,条件不足,不能确定,故③错误;④证明△EBD≌△DFC和Rt△AED≌Rt△AFD,从而得到BE=FC,AE=AF,进而可证明④正确.
解:如图所示:连接BD、DC.
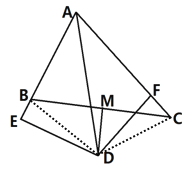
①∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∴①正确;
②∵∠EAC=60°,AD平分∠BAC,
∴∠EAD=∠FAD=30°,
∵DE⊥AB,
∴∠AED=90°,
∴ED=![]() AD,
AD,
同理:DF=![]() AD,
AD,
∴DE+DF=AD,
∴②正确;
③由题意可知:∠EDA=∠ADF=60°,
假设DM平分∠ADF,则∠ADM=30°,则∠EDM=90°,
又∵∠E=∠BMD=90°,
∴∠EBM=90°,
∴∠ABC=90°,
∵不知道∠ABC是否等于90°,
∴不能判定DM平分∠ADF,
∴③错误;
④∵DM是BC的垂直平分线,
∴DB=DC,
在Rt△BED和Rt△CFD中,![]() ,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=FC,
同理可证,Rt△AED≌Rt△AFD,
∴AE=AF,
∴AB+AC=AEBE+AF+FC=2AE,
∴④正确,
故选:C.


科目:初中数学 来源: 题型:
【题目】已知点O为直线AB上的一点,∠BOC=∠DOE=90°
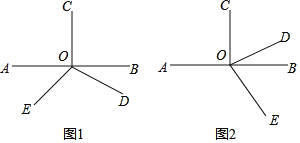
(1)如图1,当射线OC、射线OD在直线AB的两侧时,请回答结论并说明理由;
①∠COD和∠BOE相等吗?
②∠BOD和∠COE有什么关系?
(2)如图2,当射线OC、射线OD在直线AB的同侧时,请直接回答;
①∠COD和∠BOE相等吗?
②第(1)题中的∠BOD和∠COE的关系还成立吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:

(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
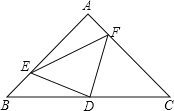
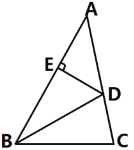
【题目】已知:三角形ABC中,∠A=90,AB=AC,D为BC的中点,如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
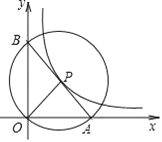
【题目】如图,在平面直角坐标系中,O 为坐标原点,P是反比例函数![]() 图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
(1)求证:P为线段AB的中点;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BD平分∠ABC,交AC于点D,DE⊥AB于点E,AB=3cm,BC=2.5cm,△ABD的面积为2cm2,则S△ABC=____________cm2。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上线段AB长2个单位长度,CD长4个单位长度,点A在数轴上表示的数是﹣10,点C在数轴上表示的数是16.若线段AB以每秒6个单位长度的速度向右匀速运动,同时线段CD以每秒2个单位长度的速度向左匀速运动.
![]()
(1)问:运动多少秒后,点B与点C互相重合?
(2)当运动到BC为6个单位长度时,则运动的时间是多少秒?
(3)P是线段AB上一点,当点B运动到线段CD上时,是否存在关系式![]() ?若存在,求线段PD的长;若不存在,请说明理由.
?若存在,求线段PD的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 点的初始位置位于数轴上表示
点的初始位置位于数轴上表示![]() 的点,现对
的点,现对![]() 点做如下移动:第
点做如下移动:第![]() 次向左移动
次向左移动![]() 个单位长度至
个单位长度至![]() 点,第
点,第![]() 次从
次从![]() 点向右移动
点向右移动![]() 个单位长度至
个单位长度至![]() 点,第
点,第![]() 次从
次从![]() 点向左移动
点向左移动![]() 个单位长度至
个单位长度至![]() 点,第
点,第![]() 次从
次从![]() 点向右移动
点向右移动![]() 个单位长度至
个单位长度至![]() 点,…,依此类推。这样第_____次移动到的点到原点的距离为
点,…,依此类推。这样第_____次移动到的点到原点的距离为![]() .
.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场销售甲、乙两种商品,它们的进价和售价如下表所示,
进价(元) | 售价(元) | |
甲 | 15 | 20 |
乙 | 35 | 43 |
(1)若该商场购进甲、乙两种商品共 100 件,恰好用去 2700 元,求购进甲、乙两种商品各多少件?
(2)该商场为使销售甲、乙两种商品共 100 件的总利润(利润=售价-进价)不少于750 元,且不超过 760 元,请你帮助该商场设计相应的进货方案.
(3)若商场销售甲、乙两种商品的总利润(利润=售价-进价)是 103 元,求销售甲、 乙两种商品多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com