
【题目】如图,数轴上线段AB长2个单位长度,CD长4个单位长度,点A在数轴上表示的数是﹣10,点C在数轴上表示的数是16.若线段AB以每秒6个单位长度的速度向右匀速运动,同时线段CD以每秒2个单位长度的速度向左匀速运动.
![]()
(1)问:运动多少秒后,点B与点C互相重合?
(2)当运动到BC为6个单位长度时,则运动的时间是多少秒?
(3)P是线段AB上一点,当点B运动到线段CD上时,是否存在关系式![]() ?若存在,求线段PD的长;若不存在,请说明理由.
?若存在,求线段PD的长;若不存在,请说明理由.
【答案】(1) 运动3秒后,点B与点C互相重合;(2) 运动![]() 或
或![]() 秒后,BC为6个单位长度;(3) 存在关系式
秒后,BC为6个单位长度;(3) 存在关系式![]() ,此时PD=
,此时PD= ![]() 或
或![]() .
.
【解析】
(1)设运动t秒后,点B与点C互相重合,列出关于t的方程,即可求解;
(2)分两种情况:①当点B在点C的左边时,②当点B在点C的右边时,分别列出关于t的方程,即可求解.
(3)设线段AB未运动时点P所表示的数为x,分别表示出运动t秒后,C点表示的数,D点表示的数,A点表示的数,B点表示的数,P点表示的数,从而表示出BD,AP,PC,PD的长,结合![]() ,得18﹣8t﹣x=4|16﹣8t﹣x|,再分两种情况:①当C点在P点右侧时,②当C点在P点左侧时,分别求解即可.
,得18﹣8t﹣x=4|16﹣8t﹣x|,再分两种情况:①当C点在P点右侧时,②当C点在P点左侧时,分别求解即可.
(1)由题意得:BC=16-(-10)-2=24,
设运动t秒后,点B与点C互相重合,则
6t+2t=24,解得:t=3.
答:运动3秒后,点B与点C互相重合;
(2)①当点B在点C的左边时,
由题意得:6t+6+2t=24
解得:t=![]() ;
;
②当点B在点C的右边时,
由题意得:6t﹣6+2t=24,
解得:t=![]() .
.
答:运动![]() 或
或![]() 秒后,BC为6个单位长度;
秒后,BC为6个单位长度;
(3)设线段AB未运动时点P所表示的数为x,
运动t秒后,C点表示的数为16﹣2t,D点表示的数为20﹣2t,A点表示的数为﹣10+6t,B点表示的数为﹣8+6t,P点表示的数为x+6t,
∴BD=20﹣2t﹣(﹣8+6t)=28﹣8t,
AP=x+6t﹣(﹣10+6t)=10+x,
PC=|16﹣2t﹣(x+6t)|=|16﹣8t﹣x|,
PD=20﹣2t﹣(x+6t)=20﹣8t﹣x=20﹣(8t+x),
∵![]() ,
,
∴BD﹣AP=4PC,
∴28﹣8t﹣(10+x)=4|16﹣8t﹣x|,
即:18﹣8t﹣x=4|16﹣8t﹣x|,
①当C点在P点右侧时,
18﹣8t﹣x=4(16﹣8t﹣x)=64﹣32t﹣4x,
∴x+8t=![]() ,
,
∴PD=20﹣(8t+x)=20﹣![]() =
=![]() ;
;
②当C点在P点左侧时,
18﹣8t﹣x=﹣4(16﹣8t﹣x)=﹣64+32t+4x,
∴x+8t=![]() ,
,
∴PD=20﹣(8t+x)=20﹣![]() =
=![]() .
.
∴存在关系式![]() ,此时PD=
,此时PD= ![]() 或
或![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=90°![]() ∠A
∠A
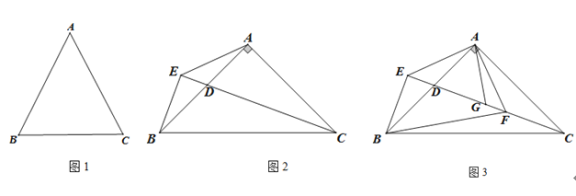
(1)如图1,求证:AB=AC;
(2)如图2,若∠BAC=90°,点D为AB上一点,过点B作直线CD的垂线,垂足为E,连接AE, 求∠AEC的度数;
(3)如图3,在(2)的条件下,过点A作AE的垂线交CE于点F,连接BF,若∠ABF-∠EAB=15°,G为DF上一点,连接AG,若∠AGD=∠EBF,AG=6,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
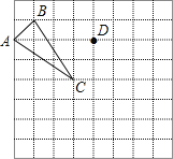
【题目】在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的三个顶点的位置。如图所示,
现将△ABC平移后得△EDF,使点B的对应点为点D,点A对应点为点E.
(1)画出△EDF;
(2)线段BD与AE有何关系? ____________;
(3)连接CD、BD,则四边形ABDC的面积为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC,现有下列结论:①DE=DF; ②DE+DF=AD; ③DM平分∠ADF; ④AB+AC=2AE,其中正确的个数有( )
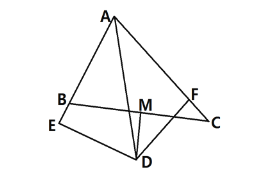
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图乙形状拼成一个正方形.

(1)你认为图乙中阴影部分的正方形的边长等于多少?
(2)请用两种不同的方法求图乙中阴影部分的面积;
(3)观察图乙,你能写出 代数式(a+b)2,(a-b)2,ab之间的等量关系吗?
(4)根据(3)题中的等量关系,解决如下问题;若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
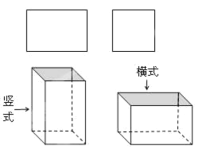
【题目】某铁件加工厂用如图所示的长方形和正方形铁片(长方形的宽与正方形的边长相等)加工成如图.所示的竖式与横式两种无盖的长方体铁容器.(加工时接缝材料不计)
(1)如果加工竖式铁容器与横式铁容器各 1 个,则共需要长方形铁片 张,正方形铁片 张.
(2)现 有长方形铁片 2017 张,正方形铁片 1178 张,如果加工成这两种铁容器,刚好铁片全部用完,那加工的竖式铁容器、横式铁容器各有多少个?
(3)把长方体铁容器加盖可以加工成为铁盒.现用 35 张铁板做成长方形铁片和正方形铁片,已知每张铁板可做成 3 个长方形铁片或 4 个正方形铁片,也可以将一张铁板裁出 1 个长方形铁片和 2 个正方形铁片.若充分利用这些铁板加工成铁盒,则最多可以加工成多少个铁盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】早在1960年、中国登山队首次从珠穆朗玛北侧中国境内登上珠峰,近几十年,珠峰更是吸引了大批的登山爱好者,某日,登山运动员傅博准备从海拔7400米的3号营地登至海拔近7900米的4号营地,由于天气骤变,近6小时的攀爬过程中他不得不几次下撤躲避强高空风,记向上爬升的海拔高度为正数,向下撒退时下降的海拔高度为负数,傅博在这一天攀爬的海拔高度记录如下:(单位:米)+320、-55、+116、-20、+81、-43、+115.
(1)傳博能按原计划在这天登至4号营地吗?
(2)若在这一登山过程中,傅博所处位置的海拔高度上升或下降1米平均消耗8大卡的卡路里,则傅博这天消耗了多少卡路里?
(3)登山消耗的卡路里预估为:1千克身体重量(体重或负重)1天需要55~65(大于等于55,小于等于65)大卡的卡路里,海拔6000米以上会使卡路里消耗增加20%,登山协会约定海拔5000米以上运动员负重14千克,在(2)的条件下,请你估算傳博的体重范围.(精确到1千克)
查看答案和解析>>
科目:初中数学 来源: 题型:
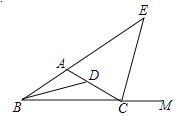
【题目】如图所示,△ABC中,BD平分∠ABC,CE平分∠ACB的邻补角∠ACM,若∠BDC=130°,∠E=50°,则∠BAC的度数是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com