
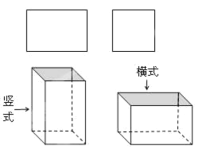
【题目】某铁件加工厂用如图所示的长方形和正方形铁片(长方形的宽与正方形的边长相等)加工成如图.所示的竖式与横式两种无盖的长方体铁容器.(加工时接缝材料不计)
(1)如果加工竖式铁容器与横式铁容器各 1 个,则共需要长方形铁片 张,正方形铁片 张.
(2)现 有长方形铁片 2017 张,正方形铁片 1178 张,如果加工成这两种铁容器,刚好铁片全部用完,那加工的竖式铁容器、横式铁容器各有多少个?
(3)把长方体铁容器加盖可以加工成为铁盒.现用 35 张铁板做成长方形铁片和正方形铁片,已知每张铁板可做成 3 个长方形铁片或 4 个正方形铁片,也可以将一张铁板裁出 1 个长方形铁片和 2 个正方形铁片.若充分利用这些铁板加工成铁盒,则最多可以加工成多少个铁盒?
【答案】(1)7,3 (2)加工的竖式铁容器有100个,横式铁容器各有539个 (3)最多可加工铁盒19个
【解析】
(1)如图得加工1个竖式铁容器需要长方形铁片4张,正方形铁片1 张;加工1个横式铁容器需要长方形铁片3张,正方形铁片2 张,即可求解.
(2)设加工的竖式铁容器有x个,横式铁容器各有y个,根据题意列出方程组求解即可.
(3)设做长方形铁片的铁板m张,做正方形铁片的铁板n张,根据题意列出方程组求解即可.
(1)如图,加工1个竖式铁容器需要长方形铁片4张,正方形铁片1 张;加工1个横式铁容器需要长方形铁片3张,正方形铁片2 张.
故如果加工竖式铁容器与横式铁容器各 1 个,则共需要长方形铁片7张,正方形铁片3 张.
(2)设加工的竖式铁容器有x个,横式铁容器各有y个,由题意得
![]()
解得![]()
故加工的竖式铁容器有100个,横式铁容器各有539个.
(3)设做长方形铁片的铁板m张,做正方形铁片的铁板n张,由题意得
![]()
解得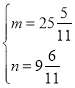
∴在这35张铁板中,25张做长方形铁片可做![]() (片),9张做正方形铁片可做
(片),9张做正方形铁片可做![]() (片),剩1张可裁出1个长方形铁片和2个正方形铁片
(片),剩1张可裁出1个长方形铁片和2个正方形铁片
共可做长方形铁片![]() (片),正方形铁片
(片),正方形铁片![]() (片)
(片)
∴可做铁盒![]() (个)
(个)
答:最多可加工铁盒19个.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
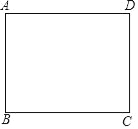
【题目】如图,矩形纸片ABCD,AD=4,AB=3,如果点E在边BC上,将纸片沿AE折叠,使点B落在点F处,联结FC,当△EFC是直角三角形时,那么BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
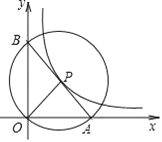
【题目】如图,在平面直角坐标系中,O 为坐标原点,P是反比例函数![]() 图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
(1)求证:P为线段AB的中点;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上线段AB长2个单位长度,CD长4个单位长度,点A在数轴上表示的数是﹣10,点C在数轴上表示的数是16.若线段AB以每秒6个单位长度的速度向右匀速运动,同时线段CD以每秒2个单位长度的速度向左匀速运动.
![]()
(1)问:运动多少秒后,点B与点C互相重合?
(2)当运动到BC为6个单位长度时,则运动的时间是多少秒?
(3)P是线段AB上一点,当点B运动到线段CD上时,是否存在关系式![]() ?若存在,求线段PD的长;若不存在,请说明理由.
?若存在,求线段PD的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:OB、OC、OM、ON是∠AOD内的射线.
(1)如图1,若∠AOD=156°,OM平分∠AOB,ON平分∠BOD,∠BOD=96°,则∠MON的度数为 .
(2)如图2,若∠AOD=m°,∠NOC=23°,OM平分∠AOB,ON平分∠BOD,求∠COM的度数(用m的式子表示);
(3)如图3,若∠AOD=156°,∠BOC=22°,∠AOB=30°,OM平分∠AOC,ON平分∠BOD,当∠BOC在∠AOD内绕着点O以2°/秒的速度逆时针旋转t秒时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 点的初始位置位于数轴上表示
点的初始位置位于数轴上表示![]() 的点,现对
的点,现对![]() 点做如下移动:第
点做如下移动:第![]() 次向左移动
次向左移动![]() 个单位长度至
个单位长度至![]() 点,第
点,第![]() 次从
次从![]() 点向右移动
点向右移动![]() 个单位长度至
个单位长度至![]() 点,第
点,第![]() 次从
次从![]() 点向左移动
点向左移动![]() 个单位长度至
个单位长度至![]() 点,第
点,第![]() 次从
次从![]() 点向右移动
点向右移动![]() 个单位长度至
个单位长度至![]() 点,…,依此类推。这样第_____次移动到的点到原点的距离为
点,…,依此类推。这样第_____次移动到的点到原点的距离为![]() .
.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积. 某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路,完成解答过程.
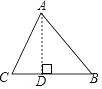
(1)作AD⊥BC于D,设BD=x,用含x的代数式表示CD,则CD=________;
(2)请根据勾股定理,利用AD作为“桥梁”建立方程,并求出x的值;
(3)利用勾股定理求出AD的长,再计算三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定x的一元一次方程ax=b的解为b﹣a,则称该方程是“差解方程”,例如:3x=4.5的解为4.5﹣3=1.5,则该方程3x=4.5就是“差解方程”,请根据上述规定解答下列问题:
(1)已知关于x的一元一次方程4x=m是“差解方程”,则m=______.
(2)已知关于x的一元一次方程4x=ab+a是“差解方程”,它的解为a,则a+b=_____.
(3)已知关于x的一元一次方程4x=mn+m和﹣2x=mn+n都是“差解方程”,求代数式﹣3(m+11)+4n+2[(mn+m)2﹣m]﹣![]() [(mn+n)2﹣2n]的值.
[(mn+n)2﹣2n]的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
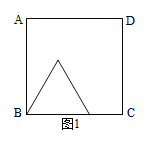
【题目】如图1,图2中,正方形ABCD的边长为6,点P从点B出发沿边BC—CD以每秒2个单位长的速度向点D匀速运动,以BP为边作等边三角形BPQ,使点Q在正方形ABCD内或边上,当点Q恰好运动到AD边上时,点P停止运动。设运动时间为t秒(t≥0)。
(1)当t=2时,点Q到BC的距离=_____;
(2)当点P在BC边上运动时,求CQ的最小值及此时t的值;
(3)若点Q在AD边上时,如图2,求出t的值;
(4)直接写出点Q运动路线的长。
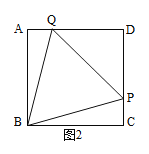
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com