
【题目】已知:OB、OC、OM、ON是∠AOD内的射线.
(1)如图1,若∠AOD=156°,OM平分∠AOB,ON平分∠BOD,∠BOD=96°,则∠MON的度数为 .
(2)如图2,若∠AOD=m°,∠NOC=23°,OM平分∠AOB,ON平分∠BOD,求∠COM的度数(用m的式子表示);
(3)如图3,若∠AOD=156°,∠BOC=22°,∠AOB=30°,OM平分∠AOC,ON平分∠BOD,当∠BOC在∠AOD内绕着点O以2°/秒的速度逆时针旋转t秒时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍,求t的值.

【答案】(1)78°;(2)![]() ;(3) 当
;(3) 当![]() 或
或![]() 时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍
时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍
【解析】
(1)由OM平分∠AOB,ON平分∠BOD,得∠BOM=30°,∠BON=48°,进而即可求解;
(2)由角平分线的定义得∠BOM=![]() ∠AOB,∠BON=
∠AOB,∠BON=![]() ∠BOD,进而得∠MON=
∠BOD,进而得∠MON=![]() ,即可求解;
,即可求解;
(3)由题意得:∠AOM═(26+t) °,∠DON=(63﹣t) °,根据∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍,列出关于t的方程,即可求解.
(1)∵∠AOD=156°,∠BOD=96°,
∴∠AOB=156°﹣96°=60°,
∵OM平分∠AOB,ON平分∠BOD,
∴∠BOM=30°,∠BON=48°,
∴∠MON=∠BOM+∠BON=78°;
(2)∵OM平分∠AOB,ON平分∠BOD,
∴∠BOM=![]() ∠AOB,∠BON=
∠AOB,∠BON=![]() ∠BOD,
∠BOD,
∵∠MON=∠BOM+∠BON=![]() (∠AOB+∠BOD)=
(∠AOB+∠BOD)= ![]() ∠AOD=
∠AOD=![]() ,
,
∴![]() ;
;
(3)∵∠BOC在∠AOD内绕点O以2°/秒的速度逆时针旋转t秒,
∴∠AOC=(52+2t) °,∠BOD=(126﹣2t) °,
∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM═(26+t) °,∠DON=(63﹣t) °,
当∠AOM=2∠DON时,26+t=2(63﹣t),则![]() ;
;
当∠DON=2∠AOM时,63﹣t=2(26+t),则t=![]() .
.
故当![]() 或
或![]() 时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍,
时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍,


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,若∠BAC=100°,则∠EAG=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边![]() 内一点
内一点![]() 将
将![]() 绕点C按顺时针方向旋转
绕点C按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() 已知
已知![]()
![]() .
.
![]() 求证:
求证:![]() 是等边三角形;
是等边三角形;
![]() 当
当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 探究:当
探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图乙形状拼成一个正方形.

(1)你认为图乙中阴影部分的正方形的边长等于多少?
(2)请用两种不同的方法求图乙中阴影部分的面积;
(3)观察图乙,你能写出 代数式(a+b)2,(a-b)2,ab之间的等量关系吗?
(4)根据(3)题中的等量关系,解决如下问题;若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
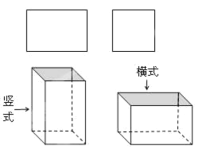
【题目】某铁件加工厂用如图所示的长方形和正方形铁片(长方形的宽与正方形的边长相等)加工成如图.所示的竖式与横式两种无盖的长方体铁容器.(加工时接缝材料不计)
(1)如果加工竖式铁容器与横式铁容器各 1 个,则共需要长方形铁片 张,正方形铁片 张.
(2)现 有长方形铁片 2017 张,正方形铁片 1178 张,如果加工成这两种铁容器,刚好铁片全部用完,那加工的竖式铁容器、横式铁容器各有多少个?
(3)把长方体铁容器加盖可以加工成为铁盒.现用 35 张铁板做成长方形铁片和正方形铁片,已知每张铁板可做成 3 个长方形铁片或 4 个正方形铁片,也可以将一张铁板裁出 1 个长方形铁片和 2 个正方形铁片.若充分利用这些铁板加工成铁盒,则最多可以加工成多少个铁盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
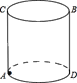
【题目】如图,圆柱的高为![]() ,底面半径为
,底面半径为![]() ,在圆柱下底面的
,在圆柱下底面的![]() 点处有一只蚂蚁,它想吃到上底面
点处有一只蚂蚁,它想吃到上底面![]() 处的食物,已知四边形
处的食物,已知四边形![]() 的边
的边![]() 、
、![]() 恰好是上、下底面的直径.为:蚂蚁至少要爬行多少路程才能食到食物?
恰好是上、下底面的直径.为:蚂蚁至少要爬行多少路程才能食到食物?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家喜欢玩的幻方游戏,老师精加创新改成了“幻圆”游戏,现在将-1,2,-3,4,5,6,- 7,8分别填入如图所示的四圈内,使横、整以及内外两圈上的4个数字之和都相等,老师已经帮助同学们完成了部分填空,则![]() 的值为( )
的值为( )
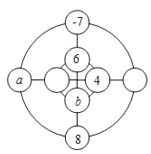
A.-8或1B.-1或1
C.-1或4D.-6或-3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有两点A、B,点A表示的数是4,点B表示的数是﹣11,点C是数轴上一动点.
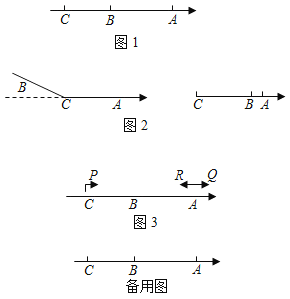
(1)如图1,若点C在点B的左侧,且BC:AB=3:5,求点C到原点的距离.
(2)如图2,若点C在A、B两点之间时,以点C为折点,将此数轴向右对折,当A、B两点之间的距离为1时,求C点在数轴上对应的数是多少?
(3)如图3,在(1)的条件下,动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度的2倍少5个单位长度/秒.经过4秒,点P、Q之间的距离是点Q、R之间距离的一半,求动点Q的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com