
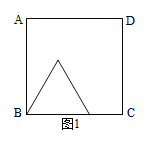
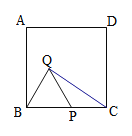
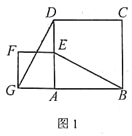
【题目】如图1,图2中,正方形ABCD的边长为6,点P从点B出发沿边BC—CD以每秒2个单位长的速度向点D匀速运动,以BP为边作等边三角形BPQ,使点Q在正方形ABCD内或边上,当点Q恰好运动到AD边上时,点P停止运动。设运动时间为t秒(t≥0)。
(1)当t=2时,点Q到BC的距离=_____;
(2)当点P在BC边上运动时,求CQ的最小值及此时t的值;
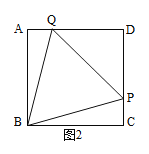
(3)若点Q在AD边上时,如图2,求出t的值;
(4)直接写出点Q运动路线的长。
【答案】(1)![]() ;(2)t=
;(2)t=![]() ,CQ=3
,CQ=3![]() ;(3)
;(3) ![]() ;(4)
;(4) ![]()
【解析】试题分析:![]() 过点
过点![]() 作
作![]() 用三角函数的知识即可求出点Q到BC的距离,
用三角函数的知识即可求出点Q到BC的距离,
![]() 点P在BC边上运动时,有
点P在BC边上运动时,有![]() ,根据垂线段最短,当
,根据垂线段最短,当![]() 时,CQ最小,作图,求解即可.
时,CQ最小,作图,求解即可.
![]() 若点Q在AD边上,则
若点Q在AD边上,则![]() 证明Rt△BAQ≌Rt△BCP,
证明Rt△BAQ≌Rt△BCP,![]()
根据![]() 列出方程求解即可.
列出方程求解即可.
![]() 点Q运动路线的长等于点
点Q运动路线的长等于点![]() 运动的路线长:
运动的路线长:![]()
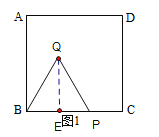
试题解析:![]() 如图:
如图:
过点![]() 作
作![]()
当![]() 时,
时,![]()
![]() 是等边三角形,
是等边三角形,
![]()
![]()
故答案为:![]()
![]() 点P在BC边上运动时,有
点P在BC边上运动时,有![]() ,根据垂线段最短,当
,根据垂线段最短,当![]() 时,CQ最小,
时,CQ最小,
如图,在直角三角形BCQ中,![]() ,
,
![]()
![]()
∴![]()
∴![]()
∴![]()
(3)若点Q在AD边上,则![]()
∵![]()
∴Rt△BAQ≌Rt△BCP(HL),
∴![]()
∴![]()
∵![]() ,且由勾股定理可得,
,且由勾股定理可得,![]()
∴![]()
解得:![]() (不合题意,舍去),
(不合题意,舍去),![]()
∴![]() .
.
(4)点Q运动路线的长等于点![]() 运动的路线长:
运动的路线长:![]()



科目:初中数学 来源: 题型:
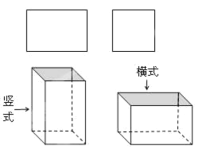
【题目】某铁件加工厂用如图所示的长方形和正方形铁片(长方形的宽与正方形的边长相等)加工成如图.所示的竖式与横式两种无盖的长方体铁容器.(加工时接缝材料不计)
(1)如果加工竖式铁容器与横式铁容器各 1 个,则共需要长方形铁片 张,正方形铁片 张.
(2)现 有长方形铁片 2017 张,正方形铁片 1178 张,如果加工成这两种铁容器,刚好铁片全部用完,那加工的竖式铁容器、横式铁容器各有多少个?
(3)把长方体铁容器加盖可以加工成为铁盒.现用 35 张铁板做成长方形铁片和正方形铁片,已知每张铁板可做成 3 个长方形铁片或 4 个正方形铁片,也可以将一张铁板裁出 1 个长方形铁片和 2 个正方形铁片.若充分利用这些铁板加工成铁盒,则最多可以加工成多少个铁盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
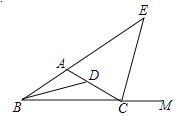
【题目】如图所示,△ABC中,BD平分∠ABC,CE平分∠ACB的邻补角∠ACM,若∠BDC=130°,∠E=50°,则∠BAC的度数是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有两点A、B,点A表示的数是4,点B表示的数是﹣11,点C是数轴上一动点.
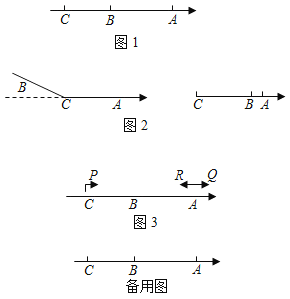
(1)如图1,若点C在点B的左侧,且BC:AB=3:5,求点C到原点的距离.
(2)如图2,若点C在A、B两点之间时,以点C为折点,将此数轴向右对折,当A、B两点之间的距离为1时,求C点在数轴上对应的数是多少?
(3)如图3,在(1)的条件下,动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度的2倍少5个单位长度/秒.经过4秒,点P、Q之间的距离是点Q、R之间距离的一半,求动点Q的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河南省旅游资源丰富,2013~2017年旅游收入不断增长,同比增速分别为:15.3%,12.7%,15.3%,14.5%,17.1%.关于这组数据,下列说法正确的是( )
A. 中位数是12.7% B. 众数是15.3%
C. 平均数是15.98% D. 方差是0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其全等的依据是( )

A.SAS B.ASA C.AAS D.SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,为了增强居民的节水意识,某自来水公司对居民用水采取以户为单位分段计费办法收费;即每月用水10吨以内(包括10吨)的用户,每吨水收费a元,每月用水超过10吨的部分,按每吨b元(b>a)收费,设一户居民月用水x(吨),应收水费y(元),y与x之间的函数关系如图所示.
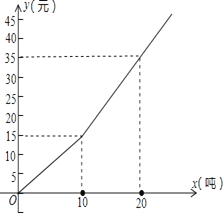
(1)分段写出y与x的函数关系式.
(2)某户居民上月用水8吨,应收水费多少元?
(3)已知居民甲上月比居民乙多用水4吨,两家一共交水费46元,求他们上月分别用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
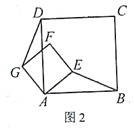
【题目】如图1,正方形ABCD和正方形AEFG,连接DG,BE。
(1)发现
当正方形AEFG绕点A旋转,如图2,①线段DG与BE之间的数量关系是____________。②直线DG与直线BE之间的位置关系是____________。
(2)探究
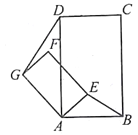
如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,证明:直线DG⊥BE
(3)应用
在(2)情况下,连结GE(点E在AB上方),若GE∥AB,且AB=![]() ,AE=1,则线段DG是多少?(直接写出结论)
,AE=1,则线段DG是多少?(直接写出结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com