
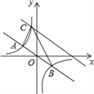
【题目】如图,在直角坐标系中,直线y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
(1)求反比例函数的表达式;
(2)将直线y=﹣![]() x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
【答案】(1) y=﹣![]() ;(2) y=﹣
;(2) y=﹣![]() x+8.
x+8.
【解析】试题分析:(1)根据题意,将y=3代入一次函数的解析式,求出x的值,得到A点的坐标,再利用反比例函数的坐标特征求出反比例函数的解析式;
(2)根据A、B点关于原点对称,可求出B点的坐标及线段AB的长度,设出平移后的直线解析式,根据平行线间的距离,由三角形的面积求出关于b的一元一次方程即可求解.
试题解析:(1)令一次函数y=﹣![]() x中y=3,则3=﹣
x中y=3,则3=﹣![]() x,
x,
解得:x=﹣6,即点A的坐标为(﹣6,3).
∵点A(﹣6,3)在反比例函数y=![]() 的图象上,
的图象上,
∴k=﹣6×3=﹣18,
∴反比例函数的表达式为y=﹣![]() .
.
(2)设平移后直线于y轴交于点F,连接AF、BF如图所示.
设平移后的解析式为y=﹣![]() x+b,
x+b,
∵该直线平行直线AB,
∴S△ABC=S△ABF,
∵△ABC的面积为48,
∴S△ABF=![]() OF(xB﹣xA)=48,
OF(xB﹣xA)=48,
由对称性可知:xB=﹣xA,
∵xA=﹣6,
∴xB=6,
∴![]() b×12=48,
b×12=48,
∴b=8.
∴平移后的直线的表达式为:y=﹣![]() x+8.
x+8.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】某公司全体职工的月工资如下:
月工资(元) | 18000 | 12000 | 8000 | 6000 | 4000 | 2500 | 2000 | 1500 | 1200 |
人数 | 1(总经理) | 2(副总经理) | 3 | 4 | 10 | 20 | 22 | 12 | 6 |
该公司月工资数据的众数为2000,中位数为2250,平均数为3115,极差为16800,公司的普通员工最关注的数据是( )
A. 中位数和众数B. 平均数和众数
C. 平均数和中位数D. 平均数和极差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组开展了一次课外活动,过程如下:如图①,正方形ABCD中,AB=4,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.
(1)求证:AP=CQ;
(2)如图②,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;
(3)在(2)的条件下,若AP=1,求PE的长.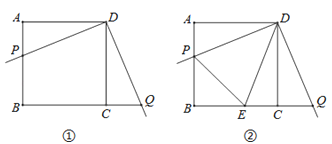
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D,CE是△ABC的角平分线. 
(1)求∠DCE的度数.
(2)若∠CEF=135°,求证:EF∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
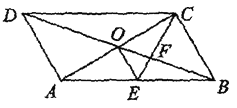
【题目】如图,平行四边形ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB丁点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列四个结论:①∠ACD=30°;②![]() ;③
;③![]() =Ac·AD;④OE:OA=1:
=Ac·AD;④OE:OA=1: ![]() 其中结论正确的序号是____.(把所有正确结论的序号都选上)
其中结论正确的序号是____.(把所有正确结论的序号都选上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com