
【题目】某校数学兴趣小组开展了一次课外活动,过程如下:如图①,正方形ABCD中,AB=4,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.
(1)求证:AP=CQ;
(2)如图②,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;
(3)在(2)的条件下,若AP=1,求PE的长.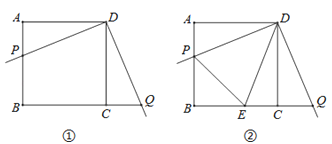
【答案】证明:(1)∵四边形ABCD是正方形,
∴∠ADC=∠A=∠B=∠BCD=∠DCQ=90°,AD=BC=CD=AB=4,
∵∠PDQ=90°,
∴∠ADP=∠CDQ,
在△APD和△CQD中,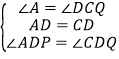 ,
,
∴△APD≌△CQD(ASA),
∴AP=CQ;
(2)解;PE=QE,理由如下:
由(1)得:△APD≌△CQD,
∴PD=QD,
∵DE平分∠PDQ,
∴∠PDE=∠QDE,
在△PDE和△QDE中,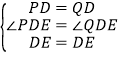 ,
,
∴△PDE≌△QDE(SAS),
∴PE=QE;
(3)解:由(2)得:PE=QE,由(1)得:CQ=AP=1,
∴BQ=BC+CQ=5,BP=AB﹣AP=3,
设PE=QE=x,则BE=5﹣x,
在Rt△BPE中,由勾股定理得:32+(5﹣x)2=x2 ,
解得:x=3.4,
即PE的长为3.4.
【解析】(1)由正方形的性质得出∠ADC=∠A=∠B=∠BCD=∠DCQ=90°,AD=BC=CD=AB=4,证出∠ADP=∠CDQ,由ASA证明△APD≌△CQD,得出对应边相等即可;
(2)由全等三角形的性质得出PD=QD,证出∠PDE=∠QDE,由SAS证明△PDE≌△QDE,得出对应边相等即可;
(3)由(2)和(1)得出PE=QE,CQ=AP=1,求出BQ=BC+CQ=5,BP=AB﹣AP=3,设PE=QE=x,则BE=5﹣x,在Rt△BPE中,由勾股定理得出方程,解方程即可.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM.
(1)当AN平分∠MAB时,求DM的长;
(2)连接BN,当DM=1时,求△ABN的面积;
(3)当射线BN交线段CD于点F时,求DF的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
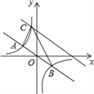
【题目】如图,在直角坐标系中,直线y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
(1)求反比例函数的表达式;
(2)将直线y=﹣![]() x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(﹣1,y2),C(2,y3)在函数y=﹣x2﹣2x+b的图象上,则y1、y2、y3的大小关系为( )
A.y1<y3<y2
B.y3<y1<y2
C.y3<y2<y1
D.y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”,为此,某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
A组:t<0.5h;B组:0.5h≤t<1h;C组:1h≤t<1.5h;D组:t≥1.5h
请根据上述信息解答下列问题:
(1)C组的人数是,并补全直方图;
(2)本次调查数据的中位数落在哪组内?
(3)若该辖区约有24000名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com