
【题目】如图所示,∠B=∠OAF=90°,BO=3cm,AB=4cm,AF=12cm,求图中半圆的面积.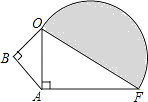
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】探究题: ![]() =3,
=3, ![]() =0.5,
=0.5, ![]() =6,
=6, ![]() =
= ![]() ,
, ![]() =0.
=0.
根据以上算式,回答:
(1)![]() 一定等于a吗?如果不是,那么
一定等于a吗?如果不是,那么 ![]() =;
=;
(2)利用你总结的规律,计算: ①若x<2,则 ![]() =;
=;
② ![]() = .
= .
(3)若a,b,c为三角形的三边长,化简: ![]() +
+ ![]() +
+ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( ) 
A.两点确定一条直线
B.两点之间线段最短
C.垂线段最短
D.在同一平面内,过一点有且只有一条直线与已知直线垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司全体职工的月工资如下:
月工资(元) | 18000 | 12000 | 8000 | 6000 | 4000 | 2500 | 2000 | 1500 | 1200 |
人数 | 1(总经理) | 2(副总经理) | 3 | 4 | 10 | 20 | 22 | 12 | 6 |
该公司月工资数据的众数为2000,中位数为2250,平均数为3115,极差为16800,公司的普通员工最关注的数据是( )
A. 中位数和众数B. 平均数和众数
C. 平均数和中位数D. 平均数和极差
查看答案和解析>>
科目:初中数学 来源: 题型:
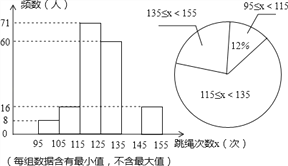
【题目】在我市开展的“阳光体育”跳绳活动中,为了了解中学生跳绳活动的开展情况,随机抽查了全市八年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制两个不完整的统计图.请根据图中提供的信息,解答下列问题:
(1)本次共抽查了多少名学生?
(2)请补全频数分布直方图空缺部分,直接写出扇形统计图中跳绳次数范围135≤x≤155所在扇形的圆心角度数.
(3)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全市8000名八年级学生中有多少名学生的成绩为优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组开展了一次课外活动,过程如下:如图①,正方形ABCD中,AB=4,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.
(1)求证:AP=CQ;
(2)如图②,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;
(3)在(2)的条件下,若AP=1,求PE的长.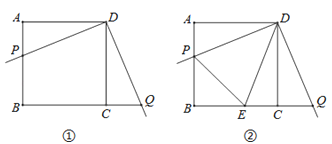
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com