
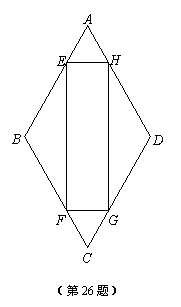
(1)已知:如图,E、F、G、H分别是菱形ABCD的各边上与顶点均不重合的点,且AE=CF=CG=AH.
求证:四边形EFGH是矩形.
 |
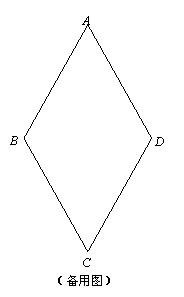
(2)已知: E、F、G、H分别是菱形ABCD的边AB、BC、CD、AD上与顶点均不重合的点,且四边形EFGH是矩形.AE与AH相等吗?如果相等,请说明理由;如果不相等,请举反例进行说明.
 |
(1)证明:∵四边形ABCD是菱形,
∴ AB=BC=CD=DA,∠A=∠C,∠B=∠D,∠A+∠B=180°.
∵ AE=CF=CG=AH,
∴ BE=BF=DG=DH.
 ∴ △AEH≌△CFG,△BEF≌△DHG.
∴ △AEH≌△CFG,△BEF≌△DHG.
∴ EH=FG,EF=HG.
∴四边形EFGH是平行四边形.
又∵∠AEH=∠AHE=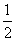 (180°-∠A)=90°-
(180°-∠A)=90°-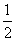 ∠A,
∠A,
∠BEF=∠BFE=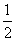 (180°-∠B)=90°-
(180°-∠B)=90°-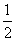 ∠B,
∠B,
∴∠HEF=180°-∠AEH-∠BEF
=180°-(90°-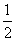 ∠A)-(90°-
∠A)-(90°-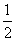 ∠B)
∠B)
=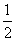 (∠A+∠B)
(∠A+∠B)
=90°.
∴四边形EFGH是矩形.
(2)如图,m、n是经过菱形对角线交点且与对边垂直的2条直线,可证四边形EFGH是矩形,显然,AE与AH不相等.


科目:初中数学 来源: 题型:
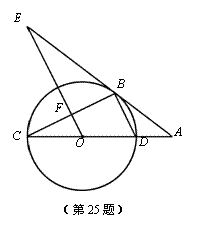
如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AE于点E.
(1)求证:∠E=∠BCO;
(2)若⊙O的半径为3,cosA=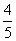 ,求EF的长.
,求EF的长.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
某纪念币从2013年11月11日起开始上市,通过市场调查得知该纪念币每1枚的市场价y(单位:元)与上市时间x(单位:天)的数据如下:
| 上市时间x天 | 4 | 10 | 36 |
| 市场价y元 | 90 | 51 | 90 |
(1)根据上表数据,在某一特定时期内,可从下列函数中选取一个恰当的函数描述纪念币的市场价y与上市时间x的变化关系:
① y=ax+b(a≠0); ② y=a(x-h)2+k( a≠0); ③ y=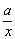 (a≠0).
(a≠0).
你可选择的函数的序号是 .
(2)利用你选取的函数,求该纪念币上市多少天时市场价最低,最低价格是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
在 ABCD中,点E在AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F.若△FDE的周长为8,△FCB的周长为22,则FC的长.为( )
ABCD中,点E在AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F.若△FDE的周长为8,△FCB的周长为22,则FC的长.为( )
A.6 B.8 C.7 D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com