
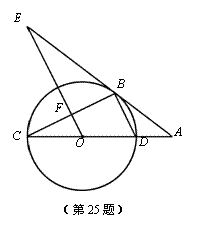
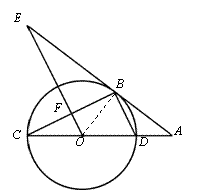
如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AE于点E.
(1)求证:∠E=∠BCO;
(2)若⊙O的半径为3,cosA=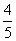 ,求EF的长.
,求EF的长.
 |
 (1)证明:连接BO.
(1)证明:连接BO.
∵OE∥BD,
∴∠E=∠ABD.
∵AE与⊙O相切于点B,∴OB⊥AE.
∴∠ABD+∠OBD=90°.
∵CD是⊙O的直径,
∴∠CBO+∠OBD=90°.
∴∠ABD=∠CBO.
∵OB=OC,
∴∠CBO=∠BCO.
∴∠E=∠BCO. 4分
(2)解:在Rt△ABO中,cosA=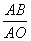 =
=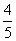 ,可设AB=4k,AO=5k,
,可设AB=4k,AO=5k,
BO=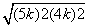 =3k.
=3k.
∵⊙O的半径为3,∴3k=3,∴k=1.
∴AB=4,AO=5.
∴AD=AO-OD=5-3=2.
∵BD∥EO,
∴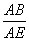 =
=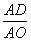 =
=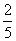 ,∴AE=10.
,∴AE=10.
∴EB=AE-AB=6.
在Rt△EBO中,EO=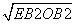 =3
=3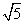 .
.
∵OE∥BD,
∴∠EFB=∠DBF=90°.
∵∠FEB=∠BEO,∠EFB=∠EBO,
∴△EFB∽△EBO.
∴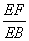 =
=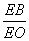 ,即
,即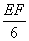 =
=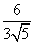 .
.
∴EF=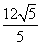 . 9分
. 9分


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
从南京到某市可乘坐普通列车,行驶路程是520千米;也可乘坐高铁,行驶路
程是400千米.已知高铁的平均速度是普通列车平均速度的2.5倍,且从南京到该市
乘坐高铁比乘坐普通列车要少用3小时.求高铁行驶的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,ON⊥OM,等腰直角三角形ACB中,∠ACB=90°,边AC在OM上,将△ACB绕点A逆时针旋转75°,使得点B的对应点E恰好落在ON上,则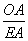 = .
= .


查看答案和解析>>
科目:初中数学 来源: 题型:
在一个不透明的口袋里装有四个球,这四个球上分别标记数字-3、-1、0、2,除数字不同外,这四个球没有任何区别.
(1)从中任取一球,求该球上标记的数字为正数的概率;
(2)从中任取两球,将两球上标记的数字分别记为x、y,求点(x,y)位于第二象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)已知:如图,E、F、G、H分别是菱形ABCD的各边上与顶点均不重合的点,且AE=CF=CG=AH.
求证:四边形EFGH是矩形.
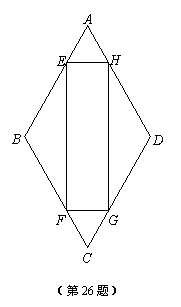 |
(2)已知: E、F、G、H分别是菱形ABCD的边AB、BC、CD、AD上与顶点均不重合的点,且四边形EFGH是矩形.AE与AH相等吗?如果相等,请说明理由;如果不相等,请举反例进行说明.
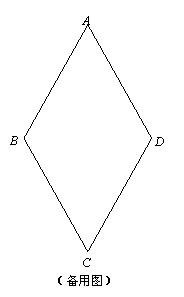 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com