
【题目】如图,正方形ABCD中,P为AB中点,BE⊥DP交DP延长线于E,连结AE,AF⊥AE交DP于F,连结BF,CF.下列结论:①EF=![]() AF;②AB=FB;③CF∥BE;④EF=CF.其中正确的结论有( )个.
AF;②AB=FB;③CF∥BE;④EF=CF.其中正确的结论有( )个.
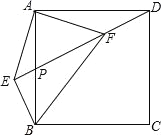
A.1 B.2 C.3 D.4
【答案】D
【解析】
试题分析:根据已知和正方形的性质推出∠EAB=∠DAF,∠EBA=∠ADP,AB=AD,证△ABE≌△ADF即可;取EF的中点M,连接AM,推出AM=MF=EM=DF,证∠AMB=∠FMB,BM=BM,AM=MF,推出△ABM≌△FBM即可;求出∠FDC=∠EBF,推出△BEF≌△DFC即可.
在正方形ABCD中,AB=AD,∠BAD=90°, ∴∠DAF+∠BAF=90°, ∵AF⊥AE,
∴∠BAE+∠BAF=90°, ∴∠BAE=∠DAF, ∵BE⊥DP, ∴∠ABE+∠BPE=90°,
又∵∠ADF+∠APD=90°,∠BPE=∠APD, ∴∠ABE=∠ADF, 在△ABE和△ADF中,
∴△ABE≌△ADF(ASA), ∴AE=AF, ∴△AEF是等腰直角三角形,
∴EF=![]() AF;故①正确; ∴AE=AF,BE=DF, ∴∠AEF=∠AFE=45°,取EF的中点M,连接AM,
AF;故①正确; ∴AE=AF,BE=DF, ∴∠AEF=∠AFE=45°,取EF的中点M,连接AM,
∴AM⊥EF,AM=EM=FM, ∴BE∥AM, ∵AP=BP, ∴AM=BE=DF, ∴∠EMB=∠EBM=45°,
∴∠AMB=90°+45°=135°=∠FMB, 在△ABM和△FBM中, ∴△ABM≌△FBM(SAS),
∴AB=BF,故②正确; ∴∠BAM=∠BFM, ∵∠BEF=90°,AM⊥EF,
∴∠BAM+∠APM=90°,∠EBF+∠EFB=90°, ∴∠APF=∠EBF, ∵AB∥CD, ∴∠APD=∠FDC,
∴∠EBF=∠FDC, 在△BEF和△DFC中, ∴△BEF≌△DFC(SAS),
∴CF=EF,∠DFC=∠FEB=90°, 故④正确; ∴CF⊥DEP, ∵BE⊥DP, ∴CF∥BE;故③正确.



 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( ) 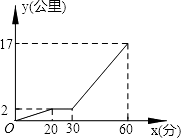
A.小强从家到公共汽车站步行了2公里
B.小强在公共汽车站等小明用了10分钟
C.公共汽车的平均速度是30公里/小时
D.小强乘公共汽车用了20分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张扑克牌的牌面如图1,将扑克牌洗匀后,如图2背面朝上放置在桌面上,小明和小亮设计了A、B两种游戏方案:
方案A:随机抽一张扑克牌,牌面数字为5时小明获胜;否则小亮获胜.
方案B:随机同时抽取两张扑克牌,两张牌面数字之和为偶数时,小明获胜;否则小亮获胜.
请你帮小亮选择其中一种方案,使他获胜的可能性较大,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当 x=﹣1 时,代数式 2ax3﹣3bx+8 的值为 18,这时 6b﹣4a+2 的值为( )
A. 20 B. 22 C. ﹣18 D. ﹣22
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读探索题:
(1)如图1,OP是∠MON的平分线,以O为圆心任意长为半径作弧,交射线ON,OM为C,B两点,在射线OP上任取一点A(O点除外),连接AB,AC,求证:△AOB≌△AOC.
(2)请你参考这个作全等三角形的方法,解答下列问题:
①如图2:在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系;
②如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9,求AB的长.
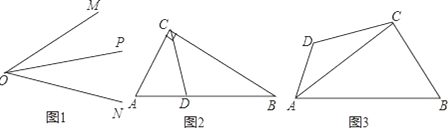
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣2,0)和点B(4,0),与y轴交于点C(0,﹣4).
(1)求二次函数的解析式,并写出抛物线的对称轴,顶点坐标;
(2)设E时抛物线对称轴上一点,当∠BEC=90°时,求点E的坐标;
(3)若P(m,n)是抛物线上一个动点(其中m>0,n<0),是否存在这样的点P,使得△PBC的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.
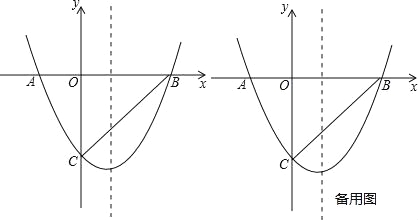
查看答案和解析>>
科目:初中数学 来源: 题型:
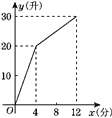
【题目】一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的部分关系如图所示.那么,从关闭进水管起________分钟该容器内的水恰好放完.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com