
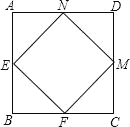
【题目】E、F、M、N分别是正方形ABCD四条边上的点,AE=BF=CM=DN,四边形EFMN是什么图形?证明你的结论.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
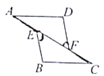
A. ∠A=∠C B. AD∥BC C. BE=DF D. AD=CB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 在平面直角坐标系中,
在平面直角坐标系中, ![]() ,
,![]() ,把矩形
,把矩形![]() 沿直线
沿直线![]() 对折使点
对折使点![]() 落在点
落在点![]() 处,直线
处,直线![]() 与
与![]() 的交点分别为
的交点分别为![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在坐标平面内,若四边形
在坐标平面内,若四边形![]() 是菱形,则菱形
是菱形,则菱形![]() 的面积是( )
的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形纸片ABCD中,AB=m,AD=n,将两张边长分别为6和4的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.
(1)在图1中,EF=___,BF=____;(用含m的式子表示)
(2)请用含m、n的式子表示图1,图2中的S1,S2,若m-n=2,请问S2-S1的值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底部未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分周长和是_________(用代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E,连接AG.
(1)求证:AG=CG;
(2)求证:AG2=GE·GF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com