Question

【题目】如图,将边长为4的正方形纸片沿折叠,点落在边上的点处,点与点重合, 与交于点,取的中点，连接,则的周长最小值是__________．

Answer 1

【答案】

【解析】

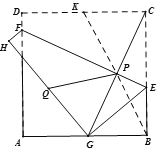
如图，取CD中点K，连接PK，PB，则CK=2，由折叠的性质可得PG=PC，GH=DC=4，PQ=PK，BP=PG，QG=2，要求△PGQ周长的最小值，只需求PQ+PG的最小值即可，即求PK+PB的最小值，观察图形可知，当K、P、B共线时，PK+PB的值最小，据此根据勾股定理进行求解即可得答案.

如图，取CD中点K，连接PK，PB，

则CK==2，

∵四边形ABCD是正方形，∴∠ABC=90°，

∵将边长为4的正方形ABCD纸片沿EF折叠，点C落在AB边上的点G处，点D与点H重合， CG与EF交于点P，取GH的中点Q，

∴PG=PC，GH=DC=4，PQ=PK，

∴BP=PG，QG=2，

要求△PGQ周长的最小值，只需求PQ+PG的最小值即可，

即求PK+PB的最小值，

观察图形可知，当K、P、B共线时，PK+PB的值最小，

此时，PK+PB=BK=，

∴△PGQ周长的最小值为：PQ+PG+QG= PK+PB+QG=BK+QG=2+2，

故答案为：2+2.