【题目】如图，小刚将一个正方形纸片剪去一个宽为5cm的长条后，再从剩下的长方形纸片上剪去一个宽为6cm的长条，如果两次剪下的长条面积正好相等，求两个所剪下的长条的面积之和为（ ）
A.215cm2B.250cm2C.300cm2D.320cm2
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】已知：如图，△ABC中，AC=BC，以BC为直径的⊙O交AB于点D，过点D作DE⊥AC于点E，交BC的延长线于点F．
求证：
（1）AD=BD；
（2）DF是⊙O的切线．
查看答案和解析>>
科目：初中数学 来源： 题型：
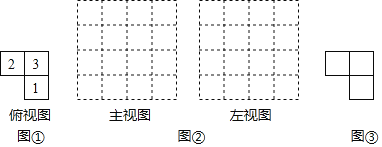
【题目】由几个相同的边长为1的小立方块搭成的几何体的俯视图如图①，格中的数字表示该位置的小立方块的个数．
（1）请在下面方格纸图②中分别画出这个几何体的主视图和左视图．
（2）根据三视图，这个组合几何体的表面积为多少个平方单位？（包括底面积）
（3）若上述小立方块搭成的几何体的俯视图不变，如图③，各位置的小立方块个数可以改变（总数目不变），则搭成这样的组合几何体中的表面积最大（包括底面积）仿照图①，将数字填写在图③的正方形中．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校数学课外小组，在坐标纸上为学校的一块空地设计植树方案如下：第k棵树种植在点Pk(xk,yk)处，其中x1=1，y1=1，当k≥2时，
,
，[a]表示非负实数a的整数部分，例如[2.6]=2，[0.2]=0．按此方案，则第2018棵树种植点的坐标为( )
A.（3，2018）B.（2，2019）C.（2，403）D.（3，404）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线经过A（﹣2，0），B（﹣3，3）及原点O，顶点为C．
（1）求抛物线的函数解析式．
（2）设点D在抛物线上，点E在抛物线的对称轴上，若四边形AODE是平行四边形，求点D的坐标．
（3）P是抛物线上的第一象限内的动点，过点P作PM⊥x轴，垂足是M，是否存在点p，使得以P、M、A为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将平行四边形ABCD折叠，使顶点D落在AB边上的点E处，折痕为AF，下列说法中不正确的是（ ）
A.EF∥BCB.EF＝AEC.BE＝CFD.AF＝BC
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（ ）
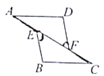
A. ∠A=∠C B. AD∥BC C. BE=DF D. AD=CB
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题情景：如图1，在等腰直角三角形ABC中∠ACB＝90°，BC＝a．将AB绕点B顺时针旋转90°得到线段BD，连接CD，过点D作△BCD的BC边上的高DE．
易证△ABC≌△BDE，从而得到△BCD的面积为
．
简单应用：如图2，在Rt△ABC中，∠ACB＝90°，BC＝a，将边AB绕点B顺时针旋转90°得到线段BD，连接CD，用含a的代数式表示△BCD的面积，并说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
