
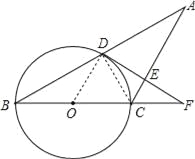
【题目】已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
求证:
(1)AD=BD;
(2)DF是⊙O的切线.

【答案】(1)证法一:连结CD,
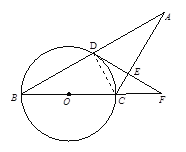
∵BC为⊙O的直径
∴CD⊥AB
∵AC=BC
∴AD=BD.
证法二:连结CD,
∵BC为⊙O的直径
∴∠ADC=∠BDC=90°
∵AC=BC,CD=CD
∴△ACD≌△BCD
∴AD=BD
(2)证法一:连结OD,

∵AD=BD,OB=OC
∴OD∥AC
∵DE⊥AC
∴DF⊥OD
∴DF是⊙O的切线.
证法二:连结OD,
∵OB=OD
∴∠BDO=∠B
∵∠B=∠A
∴∠BDO=∠A
∵∠A+∠ADE=90°
∴∠BDO+∠ADE=90°
∴∠ODF=90°
∴DF是⊙O的切线.
【解析】试题分析:(1)由于AC=AB,如果连接CD,那么只要证明出CD⊥AB,根据等腰三角形三线合一的特点,我们就可以得出AD=BD,由于BC是圆的直径,那么CD⊥AB,由此可证得.
(2)连接OD,再证明OD⊥DE即可.
试题解析:(1)连接CD,
∵BC为⊙O的直径,
∴CD⊥AB.
∵AC=BC,
∴AD=BD.
(2)连接OD;
∵AD=BD,OB=OC,
∴OD是△BCA的中位线,
∴OD∥AC.
∵DE⊥AC,
∴DF⊥OD.
∵OD为半径,
∴DF是⊙O的切线.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】一家品牌店因换季将某运动鞋打折销售,如果每双运动鞋按标价的6折出售将赚105元;而按标价的4折出售只赚21元。问:
(1)每双运动鞋的成本是多少元?
(2)为保证不亏本,最多能打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块平行四边形纸片ABCD,现将其折叠,使得AB落在AD上点F处,折痕为AE,再将△AEF沿EF翻折,若点A刚好落在CD边上点G处,则 ![]() =。
=。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】整式的加减运算:
(1)化简:-(x2+y2)+[-3xy-(x2-y2)];
(2)先化简,再求值:2(x2y+xy)-![]() (x2y-
(x2y-![]() xy)-4xy-x2y)其中x=1,y=-2
xy)-4xy-x2y)其中x=1,y=-2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2是两张形状大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,线段AB、EF的端点均在小正方形的顶点上。
(1)如图1,作出以AB为对角线的正方形;
(2)如图2,以线段EF为一边作出菱形EFGH(不是正方形),点G、H在小正方形顶点处。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2的图像向右平移2个单位,得到新的函数图像的表达式是( )
A.y=x2﹣2
B.y=(x﹣2)2
C.y=x2+2
D.y=(x+2)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,反比例函数![]() 的图象经过点A.一次函数y=kx-2的图象经过A、C两点,且与y轴交于点E.
的图象经过点A.一次函数y=kx-2的图象经过A、C两点,且与y轴交于点E.
(1)直接写出点E、C的坐标;
(2)求反比例函数的解析式;
(3)根据图象写出当x>0,且一次函数的值大于反比例函数的值时,x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了丰富学生的校园生活,准备购进一批篮球和足球.其中足球的单价比篮球的单价少20元,用900元购进的足球个数和1200元购进的篮球个数相等.
(1)篮球和足球的单价各是多少元?
(2)该校打算用800元购买篮球和足球,且两种球都必须购买,请问恰好用完800元的购买方案有哪几种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com