
【题目】如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,若四边形AODE是平行四边形,求点D的坐标.
(3)P是抛物线上的第一象限内的动点,过点P作PM⊥x轴,垂足是M,是否存在点p,使得以P、M、A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某学校为九年级数学竞赛获奖选手购买以下三种奖品,其中小笔记本每本5元,大笔记本每本7元,钢笔每支10元,购买的大笔记本的数量是钢笔数量的2倍,共花费346元,若使购买的奖品总数最多,则这三种奖品的购买数量各为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛,成绩如图所示:
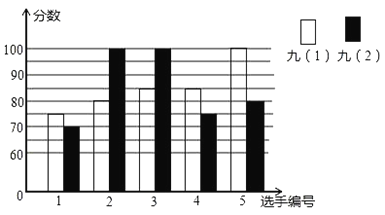
(1)根据图示填写下表;
班级 | 平均数(分) | 中位数(分) | 众数(分) |
九(1) | 85 | ||
九(2) | 85 | 100 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)已知九(1)班复赛成绩的方差是70,请计算九(2)班的复赛成绩的方差,并说明哪个班的成绩比较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,AB=AD. ∠B+∠ADC=180°,点E,F分别在四边形ABCD的边BC,CD上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系.

图1 图2 图3
(1)思路梳理
将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合.由∠B+∠ADC=180°,得∠FDG=180°,即点F,D,G三点共线. 易证△AFG![]() ,故EF,BE,DF之间的数量关系为 ;
,故EF,BE,DF之间的数量关系为 ;
(2)类比引申
如图2,在图1的条件下,若点E,F由原来的位置分别变到四边形ABCD的边CB,DC的延长线上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°. 若BD=1,EC=2,则DE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2).

(1)直接写出点C1的坐标;
(2)在图中画出△A1B1C1;
(3)求△AOA1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小刚将一个正方形纸片剪去一个宽为5cm的长条后,再从剩下的长方形纸片上剪去一个宽为6cm的长条,如果两次剪下的长条面积正好相等,求两个所剪下的长条的面积之和为( )

A.215cm2B.250cm2C.300cm2D.320cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】购买甲、乙、丙三种不同品种的练习本各四次,其中,有一次购买时,三种练习本同时打折,四次购买的数量和费用如下表:
购买次数 | 购买各种练习本的数量(单位:本) | 购买总费用(单位:元) | ||
甲 | 乙 | 丙 | ||
第一次 | 2 | 3 | 0 | 24 |
第二次 | 4 | 9 | 6 | 75 |
第三次 | 10 | 3 | 0 | 72 |
第四次 | 10 | 10 | 4 | 88 |
(1)第______次购物时打折;练习本甲的标价是_____元/本,练习本乙的标价是______元/本,练习本丙的标价是______元/本;
(2)如果三种练习本的折扣相同,请问折扣是打几折?
(3)现有资金100.5元,全部用于购买练习本,计划以标价购进练习本36本,如果购买其中两种练习本,请你直接写出一种购买方案,不需说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的发展,某快递公司为了提高分拣包裹的速度,使用机器人代替人工进行包裹分拣,若甲机器人工作![]() ,乙机器人工作
,乙机器人工作![]() ,一共可以分拣700件包裹;若甲机器人工作
,一共可以分拣700件包裹;若甲机器人工作![]() ,乙机器人工作
,乙机器人工作![]() ,一共可以分拣650件包裹.
,一共可以分拣650件包裹.
(1)求甲、乙两机器人每小时各分拣多少件包裹;
(2)去年“双十一”期间,快递公司的业务量猛增,为了让甲、乙两机器人每天分拣包裹的总数量不低于2250件,则它们每天至少要一起工作多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为节约用水,某市规定三口之家每月标准用水量为![]() 立方米,超过部分加价收费,假设不超过部分水费为
立方米,超过部分加价收费,假设不超过部分水费为![]() 元/立方米,超过部分水费为
元/立方米,超过部分水费为![]() 元/立方米.
元/立方米.
![]() 请用代数式分别表示这家按标准用水和超出标准用水各应缴纳的水费;
请用代数式分别表示这家按标准用水和超出标准用水各应缴纳的水费;
![]() 如果这家某月用水
如果这家某月用水![]() 立方米,那么该月应交多少水费?
立方米,那么该月应交多少水费?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com