【题目】随着科技的发展，某快递公司为了提高分拣包裹的速度，使用机器人代替人工进行包裹分拣，若甲机器人工作
，乙机器人工作
，一共可以分拣700件包裹；若甲机器人工作
，乙机器人工作，一共可以分拣650件包裹.
（1）求甲、乙两机器人每小时各分拣多少件包裹；
（2）去年“双十一”期间，快递公司的业务量猛增，为了让甲、乙两机器人每天分拣包裹的总数量不低于2250件，则它们每天至少要一起工作多少小时？
【答案】（1）甲、乙两机器人每小时各分拣包裹150件，100件；（2）它们每天至少要一起工作9小时.
【解析】
（1）设甲、乙两机器人每小时各分拣x件、y件包裹，根据“若甲机器人工作2h，乙机器人工作4h，一共可以分拣700件包裹；若甲机器人工作3h，乙机器人工作2h，一共可以分拣650件包裹”列出方程组，求解即可；
（2）设它们每天要一起工作t小时，根据“甲、乙两机器人每天分拣包裹的总数量不低于2250件”列出不等式，求解即可．
（1）解：设甲、乙两机器人每小时各分拣包裹
件，
件，由题意得
，
解得
.
答：甲、乙两机器人每小时各分拣包裹150件，100件．
（2）解：设它们每天至少要一起工作
小时，由题意得
，
解得
，
答：它们每天至少要一起工作9小时．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图是由几个边长为1个单位的正方体搭成的几何体.
(1)请画出这个几何体的三视图;
(2)这个几何体的体积为______个立方单位;
(3)若保持上述正方体搭成的几何体的俯视图不变，各位置的正方体个数可以改变(正方体的总数目不变),则搭成的几何体的表面积最大为_____个平方单位.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线经过A（﹣2，0），B（﹣3，3）及原点O，顶点为C．
（1）求抛物线的函数解析式．
（2）设点D在抛物线上，点E在抛物线的对称轴上，若四边形AODE是平行四边形，求点D的坐标．
（3）P是抛物线上的第一象限内的动点，过点P作PM⊥x轴，垂足是M，是否存在点p，使得以P、M、A为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（ ）
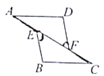
A. ∠A=∠C B. AD∥BC C. BE=DF D. AD=CB
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题情景：如图1，在等腰直角三角形ABC中∠ACB＝90°，BC＝a．将AB绕点B顺时针旋转90°得到线段BD，连接CD，过点D作△BCD的BC边上的高DE．
易证△ABC≌△BDE，从而得到△BCD的面积为
．
简单应用：如图2，在Rt△ABC中，∠ACB＝90°，BC＝a，将边AB绕点B顺时针旋转90°得到线段BD，连接CD，用含a的代数式表示△BCD的面积，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某网店销售某款童装，每件售价60元，每星期可卖300件，为了促销，该网店决定降价销售．市场调查反映：每降价1元，每星期可多卖30件．已知该款童装每件成本价40元，设该款童装每件售价x元，每星期的销售量为y件．
（1）求y与x之间的函数关系式；
（2）当每件售价定为多少元时，每星期的销售利润最大，最大利润多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,矩形
在平面直角坐标系中, 
,
,把矩形沿直线
对折使点
落在点
处,直线与
的交点分别为
,点
在
轴上,点
在坐标平面内,若四边形
是菱形,则菱形的面积是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把四张形状大小完全相同的小长方形卡片（如图①）不重叠地放在一个底面为长方形（长为m，宽为n）的盒子底部（如图②），盒子底部未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分周长和是_________（用代数式表示）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
