
【题目】已知关于x的不等式组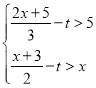 恰有三个整数解,则t的取值范围为__________.
恰有三个整数解,则t的取值范围为__________.
【答案】![]()
【解析】
先求出不等式组的解集,再根据不等式组恰有三个整数解,结合数轴,分4种情况分析讨论,分别求解即可.

解不等式①得:![]()
解不等式②得:![]()
要使不等式组有解,则![]() ,解得:
,解得:![]()
此时,![]()
则不等式组的解集为:![]()
要使不等式组恰有三个整数解,需分以下4种情况讨论:
(1)当不等式组的解集表示在数轴上如图1时,其恰好有2,3,4三个整数解
则 ,解得:
,解得: ,无公共部分,不符合题意
,无公共部分,不符合题意

(2)当不等式组的解集表示在数轴上如图2时,其恰好有3,4,5三个整数解
则 ,解得:
,解得: ,公共部分为
,公共部分为![]()

(3)当不等式组的解集表示在数轴上如图3时,其恰好有4,5,6三个整数解
则 ,解得:
,解得: ,无公共部分,不符合题意
,无公共部分,不符合题意

(4)当不等式组的解集表示在数轴上如图4时,其恰好有5,6,7三个整数解
则 ,解得:
,解得: ,无公共部分,不符合题意
,无公共部分,不符合题意

综上,当![]() 时,题干中的不等式组恰好有三个整数解
时,题干中的不等式组恰好有三个整数解
故答案为:![]() .
.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】作图与探究:
如图,已知点A、O、B是正方形网格的格点(网格线的交点),点P是∠AOB的边0B上的一点.
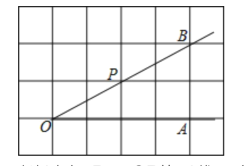
(1)过点P画OB的垂线,交OA于点E;
(2)过点P画OA的垂线,垂足为H;
(3)过点P画OA的平行线PC;
(4)若每个小正方形的边长是1,则点P到OA的距离是_________;
(5)线段PE、PH、OE的大小关系是___________(用“<"连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2).

(1)直接写出点C1的坐标;
(2)在图中画出△A1B1C1;
(3)求△AOA1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】购买甲、乙、丙三种不同品种的练习本各四次,其中,有一次购买时,三种练习本同时打折,四次购买的数量和费用如下表:
购买次数 | 购买各种练习本的数量(单位:本) | 购买总费用(单位:元) | ||
甲 | 乙 | 丙 | ||
第一次 | 2 | 3 | 0 | 24 |
第二次 | 4 | 9 | 6 | 75 |
第三次 | 10 | 3 | 0 | 72 |
第四次 | 10 | 10 | 4 | 88 |
(1)第______次购物时打折;练习本甲的标价是_____元/本,练习本乙的标价是______元/本,练习本丙的标价是______元/本;
(2)如果三种练习本的折扣相同,请问折扣是打几折?
(3)现有资金100.5元,全部用于购买练习本,计划以标价购进练习本36本,如果购买其中两种练习本,请你直接写出一种购买方案,不需说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB中,∠ABO=90°,点A位于第一象限,点O为坐标原点,点B在x轴正半轴上,若双曲线y=![]() (x>0)与△OAB的边AO、AB分别交于点C、D,点C为AO的中点,连接OD、CD.若S△OBD=3,则S△OCD为( )
(x>0)与△OAB的边AO、AB分别交于点C、D,点C为AO的中点,连接OD、CD.若S△OBD=3,则S△OCD为( )
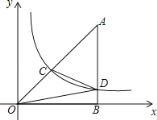
A.3B.4C.![]() D.6
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的发展,某快递公司为了提高分拣包裹的速度,使用机器人代替人工进行包裹分拣,若甲机器人工作![]() ,乙机器人工作
,乙机器人工作![]() ,一共可以分拣700件包裹;若甲机器人工作
,一共可以分拣700件包裹;若甲机器人工作![]() ,乙机器人工作
,乙机器人工作![]() ,一共可以分拣650件包裹.
,一共可以分拣650件包裹.
(1)求甲、乙两机器人每小时各分拣多少件包裹;
(2)去年“双十一”期间,快递公司的业务量猛增,为了让甲、乙两机器人每天分拣包裹的总数量不低于2250件,则它们每天至少要一起工作多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=2x的图象与反比例函数y=![]() (x>0),y=
(x>0),y=![]() (x>0)的图象分别交于P,Q两点,点P为OQ的中点,Rt△ABC的直角顶点A是双曲线y=
(x>0)的图象分别交于P,Q两点,点P为OQ的中点,Rt△ABC的直角顶点A是双曲线y=![]() (x>0)上一动点,顶点B,C在双曲线y=
(x>0)上一动点,顶点B,C在双曲线y=![]() (x>0)上,且两直角边均与坐标轴平行.
(x>0)上,且两直角边均与坐标轴平行.
(1)直接写出k的值;
(2)△ABC的面积是否变化?若不变,求出△ABC的面积;若变化,请说明理由;
(3)直线y=2x是否存在点D,使得以A,B,C,D为顶点的四边形是平行四边形,若存在,求出点A的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下面的证明过程补充完整,括号内写上相应理由或依据:已知,如图,![]() ,
,![]() ,垂足分别为D、F,
,垂足分别为D、F,![]() ,请试说明
,请试说明![]() .
.
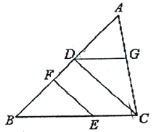
证明:∵![]() ,
,![]() (已知)
(已知)
∴![]() (____________________________)
(____________________________)
∴![]() ________(____________________________)
________(____________________________)
∴![]() ________(____________________________)
________(____________________________)
又∵![]() (已知)
(已知)
∴![]() ________(____________________________)
________(____________________________)
∴![]() ________(____________________________)
________(____________________________)
∴![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典书,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等;交易其一,金轻十三两.问金、银一枚各重几何?”意思是甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,则可列方程组为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com