
【题目】作图与探究:
如图,已知点A、O、B是正方形网格的格点(网格线的交点),点P是∠AOB的边0B上的一点.
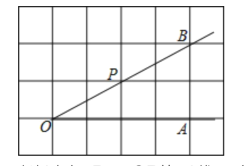
(1)过点P画OB的垂线,交OA于点E;
(2)过点P画OA的垂线,垂足为H;
(3)过点P画OA的平行线PC;
(4)若每个小正方形的边长是1,则点P到OA的距离是_________;
(5)线段PE、PH、OE的大小关系是___________(用“<"连接).
科目:初中数学 来源: 题型:
【题目】某学校为了改善办学条件,计划购置一批电子白板和一批笔记本电脑,经投标,购买1块电子白板比买3台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.
(1)求购买1块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况,需购买电子白板和笔记本电脑的总数为396,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?
(3)上面的哪种购买方案最省钱?按最省钱方案购买需要多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,六个完全相同的小长方形拼成了一个大长方形,AB是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求:①仅用无刻度直尺,②保留必要的画图痕迹.
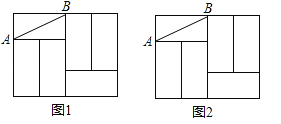
(1)在图1中画出一个45°角,使点A或点B是这个角的顶点,且AB为这个角的一边;
(2)在图2中画出线段AB的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为奖励学习之星,准备在某商店购买A、B两种文具作为奖品,已知一件A种文具的价格比一件B种文具的价格便宜5元,且用600元买A种文具的件数是用400元买B种文具的件数的2倍.
(1)求一件A种文具的价格;
(2)根据需要,该校准备在该商店购买A、B两种文具共150件.
①求购买A、B两种文具所需经费W与购买A种文具的件数a之间的函数关系式;
②若购买A种文具的件数不多于B种文具件数的2倍,且计划经费不超过2750元,求有几种购买方案,并找出经费最少的方案,及最少需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由几个边长为1个单位的正方体搭成的几何体.


(1)请画出这个几何体的三视图;
(2)这个几何体的体积为______个立方单位;
(3)若保持上述正方体搭成的几何体的俯视图不变,各位置的正方体个数可以改变(正方体的总数目不变),则搭成的几何体的表面积最大为_____个平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读并解决问题:归纳
人们通过长期观察发现,如果早晨天空中有棉絮状的高积云,那么午后常有雷雨降临,于是有了“朝有破絮云,午后雷雨临”的谚语.在数学里,我们也常用这样的方法探求规律,例如:三角形有3个顶点,如果在它的内部再画n个点,并以(n+3)个点为顶点,把三角形剪成若干个小三角形,那么最多可以剪得多少个这样的三角形? .为了解决这个问题,我们可以从n=1、n=2、nr=3 等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.

(1)完成表格信息:_______、_________;
(2)通过观察、比较,可以发现:三角形内的点每增加1个,最多可以剪得的三角形增加_________个.于是,我们可以猜想:当三角形内的点的个数为n时,最多可以剪得____________个三角形.像这样通过对现象的观察、分析,从特殊到-般地探索这类现象的规律、提出猜想的思想方法称为归纳.在日常生活中,人们互相交谈时,常常有人在列举了一些现象后,说“这(即列举的现象)说明....其实这就是运用了归纳的方法.用归纳的方法得出的结论不一定正确,是否正确需要加以证实.
(3)请你借助表格尝试用归纳的方法探索: 1+3+5+7+......+(2n-1)的和是多少?并加以证实.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com